Stationary phase, method of the

A method for calculating the asymptotics of integrals of rapidly-oscillating functions:

(*)

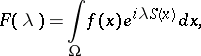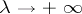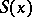where , , , is a large parameter, is a bounded domain, the function (the phase) is real, the function 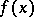is complex, and 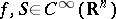. If 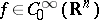, i.e. 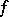has compact support, and the phase 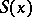does not have stationary points (i.e. points at which 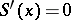) on 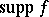, , 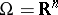then 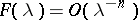, for all as 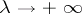. Therefore, when 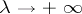, the points of stationary phase and the boundary 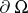give the essential contribution to the asymptotics of the integral (*). The integrals

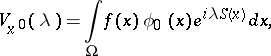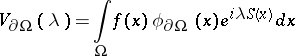are called the contributions from the isolated stationary point 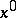and the boundary, respectively, where 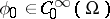, 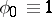near the point 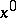and 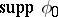does not contain any other stationary points, 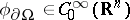and 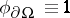in a certain neighbourhood of the boundary. For , :

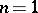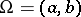1) 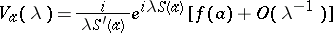, if ;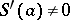

2)

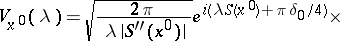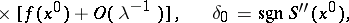if 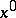is an interior point of and , .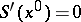

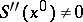Detailed research has been carried out in the case where 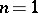, the phase 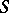has a finite number of stationary points, all of finite multiplicity, and the function 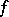has zeros of finite multiplicity at these points and at the end-points of an interval . Asymptotic expansions have been obtained. The case where the functions 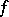and 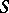have power singularities has also been studied: for example, 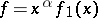, , 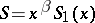where 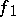, 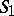are smooth functions when , , .

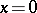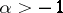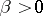Let 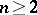, and let 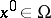be a non-degenerate stationary point (i.e. ). The contribution from the point 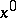is then equal to

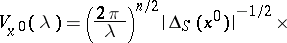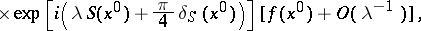where 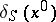is the signature of the matrix 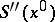. There is also an asymptotic series for 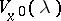(for the formulas of the contribution 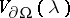in the case of a smooth boundary, see [5]).

If 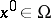is a stationary point of finite multiplicity, then (see [6])

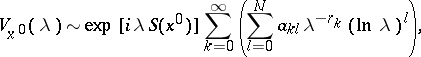where 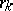are rational numbers, 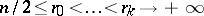. Degenerate stationary points have been studied, cf. [3], [4].

Studies have been made on the case where the phase 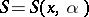depends on a real parameter 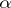, and for small 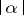has two close non-degenerate stationary points. In this case, the asymptotics of the integral 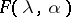can be expressed in terms of Airy functions (see [5], [10]). The method of the stationary phase has an operator variant: 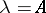, where 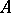is the infinitesimal operator of the strongly-continuous group 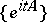of operators bounded on the axis 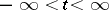, acting on a Banach space 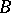, and 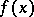, 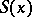are smooth functions with values in 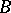[9]. If the functions are analytic, then the method of the stationary phase is a particular case of the saddle point method.

References

[1]	W. Thomson, Philos. Mag. , 23 (1887) pp. 252–255
[2]	A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956)
[3]	E.Ya. Rieksteyn'sh, "Asymptotic expansions of integrals" , 1–2 , Riga (1974–1977) (In Russian)
[4]	F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974)
[5]	M.V. Fedoryuk, "The method of steepest descent" , Moscow (1977) (In Russian)
[6]	M.F. Atiyah, "Resolution of singularities and division of distributions" Comm. Pure Appl. Math. , 23 : 2 (1970) pp. 145–150
[7]	V.I. Arnol'd, "Remarks on the stationary phase method and Coxeter numbers" Russian Math. Surveys , 28 : 5 (1973) pp. 19–48 Uspekhi Mat. Nauk , 28 : 5 (1973) pp. 17–44
[8]	A.N. Varchenko, "Newton polyhedra and estimation of oscillating integrals" Funct. Anal. Appl , 10 : 3 (1976) pp. 175–196 Funktsional. Anal. i Prilozhen. , 10 : 3 (1976) pp. 13–38
[9]	V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian)
[10]	M.V. Fedoryuk, "Asymptotics. Integrals and series" , Moscow (1987) (In Russian)

Comments

An integral of the form (*) is a special case of a so-called oscillatory integral, or Fourier integral operator, cf. also [a2].

References

[a1]	R. Wong, "Asymptotic approximations of integrals" , Acad. Press (1989)
[a2]	L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) pp. §7.7