Unipotent matrix
From Encyclopedia of Mathematics
A square matrix  over a ring for which the matrix
over a ring for which the matrix  , where
, where  is the order of
is the order of  , is nilpotent, i.e.
, is nilpotent, i.e.  . A matrix over a field is unipotent if and only if its characteristic polynomial is
. A matrix over a field is unipotent if and only if its characteristic polynomial is  .
.
A matrix group is called unipotent if every matrix in it is unipotent. Any unipotent subgroup of  , where
, where  is a field, is conjugate in
is a field, is conjugate in  to some subgroup of a special triangular group (Kolchin's theorem). This assertion is also true for unipotent groups over a skew-field, if the characteristic of the latter is either 0 or greater than some
to some subgroup of a special triangular group (Kolchin's theorem). This assertion is also true for unipotent groups over a skew-field, if the characteristic of the latter is either 0 or greater than some 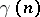 .
.
How to Cite This Entry:
Unipotent matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unipotent_matrix&oldid=15993
Unipotent matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unipotent_matrix&oldid=15993
This article was adapted from an original article by D.A. Suprunenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article