Unbounded operator

A mapping from a set in a topological vector space into a topological vector space such that there is a bounded set 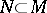whose image is an unbounded set in .

The simplest example of an unbounded operator is the differentiation operator , defined on the set of all continuously-differentiable functions into the space 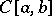of all continuous functions on 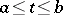, because the operator 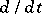takes the bounded set 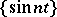to the unbounded set 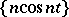. An unbounded operator is necessarily discontinuous at certain (and if 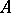is linear, at all) points of its domain of definition. An important class of unbounded operators is that of the closed operators (cf. Closed operator), because they have a property that to some extent replaces continuity.

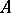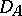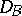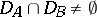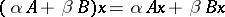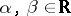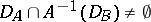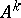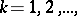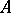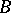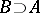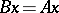Let and be unbounded operators with domains of definition and . If , then on the intersection the operator , (or ), is defined, and, similarly, if , then the operator is defined. In particular, in this way the powers , of an unbounded operator are defined. An operator is said to be an extension of an operator , , if and for 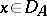. E.g., 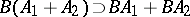. Commutativity of two operators is usually treated for the case when one of them is bounded: An unbounded operator 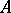commutes with a bounded operator 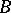if .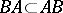

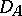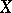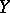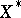For unbounded linear operators the concept of the adjoint operator is (still) defined. Let be an unbounded operator on a set which is dense in a topological vector space and mapping into a topological vector space . If and 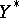are the strong dual spaces to 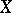and 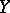, respectively, and if 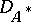is the collection of linear functionals 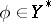for which there exists a linear functional such that for all , then the correspondence 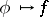determines an operator 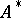on (which may, however, consists of the zero element only) in 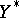, the so-called adjoint operator of .

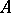References

[1]	K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1
[2]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)
[3]	F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French)
[4]	L.A. [L.A. Lyusternik] Ljusternik, "Elements of functional analysis" , Wiley & Hindustan Publ. Comp. (1974) (Translated from Russian)
[5]	J. von Neumann, "Mathematische Grundlagen der Quantenmechanik" , Dover, reprint (1943)

Comments

A continuous linear operator from one topological vector space into another maps bounded sets into bounded sets. The converse is also true for linear mappings between normed linear spaces.

References

[a1]	S. Goldberg, "Unbounded linear operators" , McGraw-Hill (1966)
[a2]	I.C. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators" , 1 , Birkhäuser (1991)