Regression spectrum

The spectrum of a stochastic process occurring in the regression scheme for a stationary time series. Thus, let a stochastic process which is observable for be represented in the form

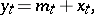(1)

where is a stationary stochastic process with , and let the mean value be expressed in the form of a linear regression

(2)

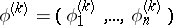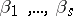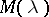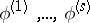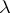where , , are known regression vectors and are unknown regression coefficients (cf. Regression coefficient). Let be the spectral distribution function of the regression vectors (cf. Spectral analysis of a stationary stochastic process). The regression spectrum for is the set of all such that 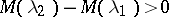for any interval 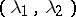containing , .

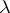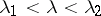The regression spectrum plays an important role in problems of estimating the regression coefficients in the scheme (1)–(2). For example, the elements of a regression spectrum can be used to express a necessary and sufficient condition for the asymptotic efficiency of an estimator for 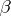by the method of least squares.

References

[1]	U. Grenander, M. Rosenblatt, "Statistical analysis of stationary time series" , Wiley (1957)