Information, source of

An object producing information that could be transmitted over a communication channel. The information produced by a source of information 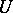is a random variable 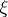defined on some probability space 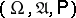, taking values in some measurable space 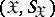, and having a probability distribution .

Usually

where are copies of one and the same measurable space and 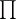is the direct product of as 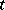runs through a set that is, a rule, either a certain interval (finite, infinite to one side, or infinite to both sides) on the real axis, or some discrete subset of this axis (usually, or 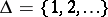). In the first of these cases one speaks of a continuous-time source of information, while in the second — of a discrete-time source of information. In other cases, a random variable 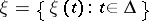with values in represents the information. In applications 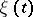is treated as the information produced by the source at the moment of time 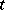. The samples of random variables 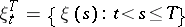are called the segments 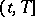of information.

Sources of information can be divided into various classes, depending on the type of information, i.e. of the random process 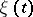produced by the source. E.g., if 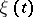is a random process with independent identically-distributed values, or if it is a stationary, an ergodic, a Markov, a Gaussian, etc., process, then the source is called a source of information without memory, or a stationary, ergodic, Markov, Gaussian, etc., source.

One of the problems in the theory of information transmission (cf. Information, transmission of) is the problem of encoding a source of information. One distinguishes between, e.g. encoding of a source by codes of fixed length, by codes of variable length, encoding under given accuracy conditions, etc. (in applications some encoding problems are called quantization of information, contraction of information, etc.). E.g., let 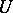be a discrete-time source of information without memory producing information with components that take values in some finite set (alphabet) . Suppose there is another finite set 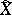(the set of values of the components 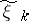of the information reproduced). An encoding of volume 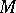of a segment of information 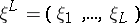of length 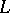is a mapping of 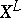into a set of 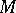elements of . 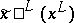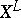Let be the image of under such a mapping ( is the direct product of 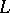copies of 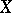). Suppose further that the exactness of reproducibility of information (cf. Information, exactness of reproducibility of) is given by a non-negative real-valued function 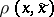, , 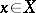, a measure of distortion, for which its average measure of distortion of encoding is given by

(1)

where

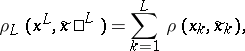if and . The quantity

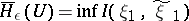(2)

is the -entropy of a source of information without memory. Here 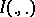is the amount of information (cf. Information, amount of), and the infimum is over all compatible distributions of pairs , , , 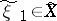for which the distribution of coincides with the distributions of the individual components of 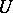and for which

The encoding theorem for a source of information. Let 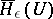be the -entropy of a discrete source 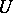without memory and with a finite measure of distortion ; let 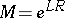. Then: 1) for any 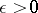, , 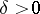, 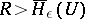and all sufficiently large 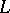, there is an encoding of volume 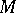of the segments of length such that the average distortion satisfies the inequality 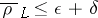; 2) if 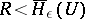, then for any encoding of volume of segments of length 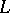the average distortion 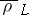satisfies the inequality 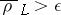. This encoding theorem can be generalized to a wide class of sources of information, e.g. to sources for which the space of values of the components is continuous. Instead of an encoding of volume 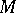one speaks in this case of quantization of volume of the source of information. It must be noted that the -entropy entering in the formulation of the theorem coincides, for and measure of distortion

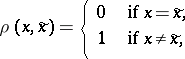as 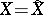, with the rate of generation of information by the given source (cf. Information, rate of generation of).

References

[1]	C. Shannon, "A mathematical theory of communication I - II" Bell. Systems Techn. J. , 27 (1948) pp. 379–423; 623–656
[2]	P.L. Dobrushin, "A general formulation of Shannon's fundamental theorem in information theory" Uspekhi Mat. Nauk , 14 : 6 (1959) pp. 3–104 (In Russian)
[3]	R. Gallagher, "Information theory and reliable communication" , Wiley (1968)
[4]	T. Berger, "Rate distortion theory" , Prentice-Hall (1971)