Bregman distance
Given a convex closed set  with non-empty interior
with non-empty interior  and a Bregman function
and a Bregman function  with zone
with zone  , the Bregman distance
, the Bregman distance  is defined as:
is defined as:
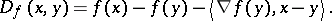 |
Bregman distances were introduced in [a1]. For several examples of Bregman distances for relevant sets 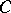 , see Bregman function. It follows easily from the properties of Bregman functions that
, see Bregman function. It follows easily from the properties of Bregman functions that 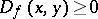 for all
for all  and all
and all 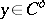 , that
, that  if and only if
if and only if  and that
and that 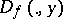 is a convex function (cf. also convex function (of a real variable)) for all
is a convex function (cf. also convex function (of a real variable)) for all  . In general,
. In general,  does not satisfy the triangle inequality, it is not symmetric (i.e. it is not true that
does not satisfy the triangle inequality, it is not symmetric (i.e. it is not true that  for all
for all  ,
,  ) and
) and 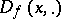 is not convex. If
is not convex. If 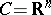 and either
and either 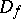 is symmetric or
is symmetric or 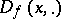 is convex for all
is convex for all  , then
, then 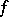 is a quadratic function and
is a quadratic function and  is the square of an elliptic norm. A basic property of Bregman distances, which follows easily from the definition, is the following:
is the square of an elliptic norm. A basic property of Bregman distances, which follows easily from the definition, is the following:
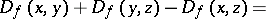 |
 |
for all  , and all
, and all 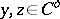 . Given a closed convex set
. Given a closed convex set 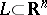 such that
such that 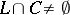 , the Bregman projection onto
, the Bregman projection onto 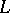 ,
, 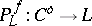 , is defined as
, is defined as
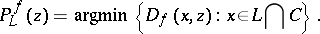 |
The properties of Bregman distances ensure existence and uniqueness of 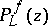 for all
for all  . Given closed convex sets
. Given closed convex sets 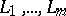 such that
such that 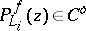 for all
for all  and all
and all 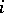 (such sets are said to be zones consistent with
(such sets are said to be zones consistent with 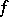 ), it is interesting to consider a sequence of successive Bregman projections onto the convex sets
), it is interesting to consider a sequence of successive Bregman projections onto the convex sets  , i.e. the sequence
, i.e. the sequence  with
with 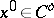 and iterative formula given by
and iterative formula given by
 |
where 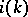 is the index of the convex set used in the
is the index of the convex set used in the 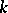 th iteration (for instance cyclically, i.e.
th iteration (for instance cyclically, i.e.  ). This algorithm, called Bregman's method, converges to a point in
). This algorithm, called Bregman's method, converges to a point in 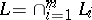 if
if 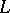 is non-empty (see [a1]). It has been proved in [a1] that if all the sets
is non-empty (see [a1]). It has been proved in [a1] that if all the sets 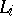 are hyperplanes, then the limit of the sequence
are hyperplanes, then the limit of the sequence 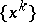 is also the unique solution of
is also the unique solution of 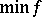 , subject to
, subject to 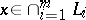 . This property also holds for an underrelaxed version of the method, of the type
. This property also holds for an underrelaxed version of the method, of the type
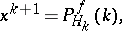 |
where 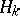 is a hyperplane parallel to
is a hyperplane parallel to 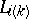 and lying between
and lying between 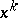 and
and 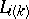 (see [a3]). Under suitable modifications in the definition of the hyperplane
(see [a3]). Under suitable modifications in the definition of the hyperplane 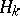 , the method has been extended to the case of minimization of
, the method has been extended to the case of minimization of 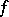 subject to linear inequalities and linear interval constraints (see [a2], [a5]). The entropy maximization method known as MART (multiplicative algebraic reconstruction technique, see [a4]) is a particular case of Bregman's method with
subject to linear inequalities and linear interval constraints (see [a2], [a5]). The entropy maximization method known as MART (multiplicative algebraic reconstruction technique, see [a4]) is a particular case of Bregman's method with  (the non-negative orthant of
(the non-negative orthant of  ) and
) and  , under a specific underrelaxation strategy.
, under a specific underrelaxation strategy.
Bregman distances have also been used to generate generalized proximal point methods for convex optimization and variational inequalities (cf. Proximal point methods in mathematical programming).
References
| [a1] | L.M. Bregman, "The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming" USSR Comput. Math. Math. Phys. , 7 : 3 (1967) pp. 200–217 (In Russian) |
| [a2] | Y. Censor, A. Lent, "An iterative row-action method for interval convex programming" J. Optimization Th. Appl. , 34 (1981) pp. 321–353 |
| [a3] | A.R. de Pierro, A.N. Iusem, "A relaxed version of Bregman's method for convex programming" J. Optimization Th. Appl. , 51 (1986) pp. 421–440 |
| [a4] | R. Gordon, R. Bender, G.T. Herman, "Algebraic reconstruction techniques (art) for three dimensional electron microscopy and x-ray photography" J. Theor. Biology , 29 (1970) pp. 471–481 |
| [a5] | A.N. Iusem, S.A. Zenios, "Interval underrelaxed Bregman method with an application" Optimization , 35 (1995) pp. 227–250 |
Bregman distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bregman_distance&oldid=15904