Inverse mapping
(inverse operator) of a single-valued onto mapping (operator)
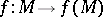 |
A single-valued mapping  such that
such that
 | (1) |
 | (2) |
where 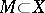 ,
, 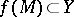 and
and 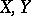 are any sets.
are any sets.
If 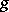 satisfies only condition (1), then it is called a left-inverse mapping of
satisfies only condition (1), then it is called a left-inverse mapping of 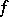 , and if it satisfies only condition (2), it is a right-inverse mapping of
, and if it satisfies only condition (2), it is a right-inverse mapping of 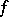 . The inverse mapping
. The inverse mapping 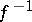 exists if and only if for each
exists if and only if for each 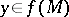 the complete inverse image
the complete inverse image  consists of a single element
consists of a single element  . If
. If 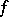 has an inverse mapping
has an inverse mapping  , then the equation
, then the equation
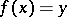 | (3) |
has a unique solution for each  . If only a right inverse
. If only a right inverse 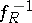 exists, then a solution of (3) exists, but its uniqueness is an open question. If only a left inverse
exists, then a solution of (3) exists, but its uniqueness is an open question. If only a left inverse 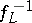 exists, then the solution is unique, assuming that it exists. If
exists, then the solution is unique, assuming that it exists. If  and
and 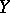 are vector spaces and if
are vector spaces and if 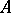 is a linear operator from
is a linear operator from  into
into 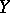 , then
, then 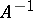 is also linear, if it exists. In general, if
is also linear, if it exists. In general, if  and
and 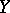 are endowed with some kind of structure, it may happen that certain properties of
are endowed with some kind of structure, it may happen that certain properties of 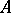 are also inherited by
are also inherited by 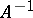 , assuming that it exists. E.g., if
, assuming that it exists. E.g., if 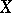 and
and 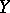 are Banach spaces and
are Banach spaces and  is a closed operator, then
is a closed operator, then 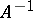 is also closed; if
is also closed; if 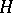 is a Hilbert space and
is a Hilbert space and  is self-adjoint, then
is self-adjoint, then 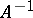 is also self-adjoint; if
is also self-adjoint; if  is an odd function, then
is an odd function, then  is also odd, etc. The continuity of
is also odd, etc. The continuity of 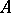 does not always imply the continuity of
does not always imply the continuity of  for many important classes of linear operators, for example for completely-continuous operators. The following are important tests for the continuity of the inverse of a linear operator.
for many important classes of linear operators, for example for completely-continuous operators. The following are important tests for the continuity of the inverse of a linear operator.
Let 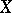 be a finite-dimensional vector space, with a certain basis, and let
be a finite-dimensional vector space, with a certain basis, and let 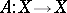 be given by the matrix
be given by the matrix 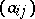 with respect to this basis. Then
with respect to this basis. Then 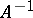 exists if and only if
exists if and only if 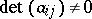 (in this case
(in this case 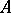 and
and 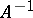 are automatically continuous).
are automatically continuous).
Let 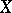 and
and 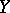 be Banach spaces, and let
be Banach spaces, and let 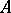 be a continuous linear operator from
be a continuous linear operator from 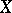 into
into  .
.
1) If  , where
, where 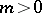 , then
, then 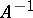 exists and is continuous.
exists and is continuous.
2) If 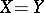 ,
, 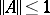 , then
, then 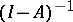 exists, is continuous and
exists, is continuous and
 |
where the series on the right-hand side converges in the norm of the space 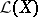 .
.
3) The operator 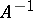 exists and is continuous on all of
exists and is continuous on all of 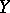 if and only if the conjugate
if and only if the conjugate 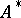 has an inverse which is defined and continuous on
has an inverse which is defined and continuous on  . Here
. Here 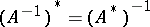 .
.
4) If  exists, is continuous and if
exists, is continuous and if 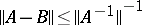 , then
, then 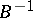 also exists, is continuous and
also exists, is continuous and
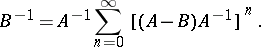 |
Thus, the set of invertible operators is open in  in the uniform topology of this space.
in the uniform topology of this space.
5) Banach's open mapping theorem: If 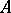 is a one-to-one mapping of
is a one-to-one mapping of 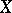 onto
onto  , then the inverse mapping, which exists, is continuous. This theorem has the following generalization: A one-to-one continuous linear mapping of a fully-complete space
, then the inverse mapping, which exists, is continuous. This theorem has the following generalization: A one-to-one continuous linear mapping of a fully-complete space 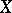 onto a separated barrelled space
onto a separated barrelled space  is a topological isomorphism.
is a topological isomorphism.
The spectral theory of linear operators on a Hilbert space contains a number of results on the existence and continuity of the inverse of a continuous linear operator. E.g., if 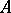 is self-adjoint and
is self-adjoint and 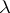 is not real, then
is not real, then  exists and is continuous.
exists and is continuous.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian) |
| [3] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
| [4] | A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) |
Inverse mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_mapping&oldid=15880