Remainder
of an expansion of a function
An additive term in a formula approximating a function by another, simpler, function. The remainder equals the difference between the given function and its approximating function, and an estimate of it is therefore an estimate of the accuracy of the approximation.
The approximating formulas alluded to include the Taylor formula, interpolation formulas, asymptotic formulas, formulas for the approximate evaluation of some quantity, etc. Thus, in the Taylor formula
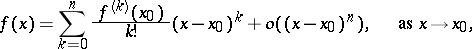 |
the term 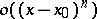 is called the remainder (in Peano's form). Given the asymptotic expansion
is called the remainder (in Peano's form). Given the asymptotic expansion
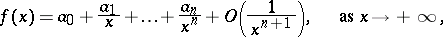 |
of a function, the remainder is 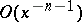 , as
, as 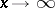 . In the Stirling formula, which gives an asymptotic expansion of the Euler gamma-function,
. In the Stirling formula, which gives an asymptotic expansion of the Euler gamma-function,
 |
the remainder is  .
.
Comments
The remainder of an integer  upon division by a natural number
upon division by a natural number 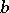 is the number
is the number  ,
, 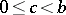 , for which
, for which  with
with  an integer. See also Remainder of an integer.
an integer. See also Remainder of an integer.
References
| [a1] | N. Bleistein, R.A. Handelsman, "Asymptotic expansions of integrals" , Dover, reprint (1986) pp. Chapts. 1, 3, 5 |
| [a2] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a3] | M. Spivak, "Calculus" , Benjamin (1967) |
Remainder. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Remainder&oldid=15868