Retract
of an object of a category
A concept generalizing the corresponding concepts in algebra and topology. An object 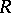 of a category
of a category 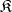 is called a retract of an object
is called a retract of an object 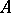 if there exist morphisms
if there exist morphisms
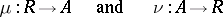 |
such that 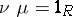 . The morphism
. The morphism  in this case is a monomorphism and, moreover, the equalizer of the pair of morphisms
in this case is a monomorphism and, moreover, the equalizer of the pair of morphisms 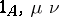 . Dually, the morphism
. Dually, the morphism  is an epimorphism and also the co-equalizer of the pair of morphisms
is an epimorphism and also the co-equalizer of the pair of morphisms 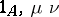 .
. 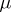 is sometimes known as a section and
is sometimes known as a section and  as a retraction.
as a retraction.
If 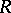 is a retract of an object
is a retract of an object 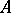 and an object
and an object 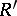 is isomorphic to
is isomorphic to 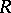 , then
, then 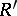 is a retract of
is a retract of 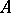 . Therefore an isomorphism class of retracts forms a single subobject of
. Therefore an isomorphism class of retracts forms a single subobject of 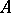 . Each retract of
. Each retract of 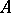 , defined by morphisms
, defined by morphisms 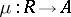 and
and 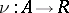 , corresponds to an idempotent morphism
, corresponds to an idempotent morphism 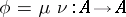 . Two retracts
. Two retracts 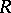 and
and 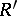 of an object
of an object 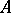 belong to the same subobject if and only if they correspond to the same idempotent. The retracts of any object of an arbitrary category form a set.
belong to the same subobject if and only if they correspond to the same idempotent. The retracts of any object of an arbitrary category form a set.
Comments
The last sentence above is true only if one assumes that all categories involved are locally small (i.e. "have small hom-sets" ) (cf. also Small category).
Retract. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Retract&oldid=15860