Inner product
scalar product, dot product,  of two non-zero vectors
of two non-zero vectors  and
and 
The product of their lengths and the cosine of the angle  between them:
between them:
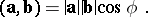 |
 is taken to be that angle between the vectors not exceeding
is taken to be that angle between the vectors not exceeding  . When
. When  or
or  is zero, the inner product is taken to be zero. The inner product
is zero, the inner product is taken to be zero. The inner product  is called the scalar square of the vector
is called the scalar square of the vector  (see Vector algebra).
(see Vector algebra).
The inner product of two  -dimensional vectors
-dimensional vectors 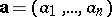 and
and  over the real numbers is given by
over the real numbers is given by
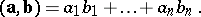 |
In the complex case it is given by
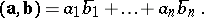 |
An infinite-dimensional vector space admitting an inner product and complete with respect to it is called a Hilbert space.
Comments
More generally, an inner product on a real vector space is a symmetric bilinear form  which is positive definite, i.e.,
which is positive definite, i.e.,  for all
for all  . A (unitary) inner product on a complex vector space is likewise defined as a Hermitian (i.e., with
. A (unitary) inner product on a complex vector space is likewise defined as a Hermitian (i.e., with  ) sesquilinear form, with complex conjugation as automorphism, which is positive definite. In finite-dimensional spaces one can always find an orthonormal basis in which
) sesquilinear form, with complex conjugation as automorphism, which is positive definite. In finite-dimensional spaces one can always find an orthonormal basis in which  takes the standard form
takes the standard form 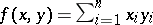 , respectively
, respectively 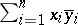 .
.
Besides the inner product (which can be defined in arbitrary dimensions), in three-dimensional space one also has the vector product.
References
| [a1] | V.I. Istrăţescu, "Inner product structures" , Reidel (1987) |
Inner product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inner_product&oldid=15855