Inter-quantile width
inter-quantile distance, inter-quantile range
The difference between the lower and upper quantiles of the same level (cf. Quantile). Let 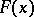 be a strictly-monotone continuous distribution function and let
be a strictly-monotone continuous distribution function and let 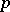 be an arbitrary number,
be an arbitrary number, 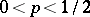 . The inter-quantile distance at level
. The inter-quantile distance at level 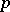 is defined as
is defined as 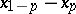 , where
, where 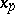 and
and 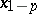 are the solutions of
are the solutions of 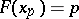 and
and  , respectively. Inter-quantile distances at well-chosen levels
, respectively. Inter-quantile distances at well-chosen levels 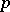 are used in mathematical statistics and probability theory to characterize the dispersion (scatter) of probability distributions. E.g., the difference
are used in mathematical statistics and probability theory to characterize the dispersion (scatter) of probability distributions. E.g., the difference 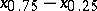 , corresponding to
, corresponding to  , has the name inter-quartile distance, and in the case of a normal distribution it is equal to
, has the name inter-quartile distance, and in the case of a normal distribution it is equal to 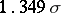 (where
(where 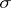 is the natural measure of dispersion, called the standard deviation); half the inter-quartile (inter-decile) is called the probable deviation (probable error or semi-inter-quartile distance). If
is the natural measure of dispersion, called the standard deviation); half the inter-quartile (inter-decile) is called the probable deviation (probable error or semi-inter-quartile distance). If 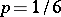 or
or 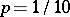 , the inter-quantile distance is called the inter-sixtile or inter-tentile, respectively.
, the inter-quantile distance is called the inter-sixtile or inter-tentile, respectively.
References
| [1] | G.U. Yale, "An introduction to the theory of statistics" , Griffin (1916) |
Inter-quantile width. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inter-quantile_width&oldid=15850