Reflection
A mapping  of an
of an  -dimensional simply-connected space
-dimensional simply-connected space  of constant curvature (i.e. of a Euclidean or affine space
of constant curvature (i.e. of a Euclidean or affine space  , a sphere
, a sphere  or a hyperbolic (Lobachevskii) space
or a hyperbolic (Lobachevskii) space  ) the set of fixed points
) the set of fixed points  of which is an
of which is an  -dimensional hyperplane. The set
-dimensional hyperplane. The set  is called the mirror of the mapping
is called the mirror of the mapping  ; in other words,
; in other words,  is a reflection in
is a reflection in 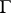 . Every reflection is uniquely defined by its mirror. The order (period) of a reflection in the group of all motions of
. Every reflection is uniquely defined by its mirror. The order (period) of a reflection in the group of all motions of 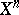 is equal to 2, i.e.
is equal to 2, i.e.  .
.
The Euclidean or affine space 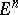 can be identified with the vector space
can be identified with the vector space 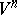 of its parallel translations. The mapping
of its parallel translations. The mapping 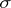 is then a linear orthogonal transformation of
is then a linear orthogonal transformation of 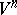 with matrix
with matrix
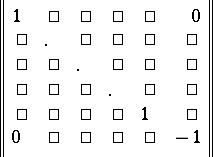 |
in a certain orthonormal basis, and conversely, every orthogonal transformation of  with this matrix in a certain orthonormal basis is a reflection in
with this matrix in a certain orthonormal basis is a reflection in 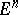 . More generally, a linear transformation
. More generally, a linear transformation 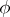 of an arbitrary vector space
of an arbitrary vector space 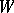 over a field
over a field 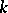 , of characteristic other than 2, is called a linear reflection if
, of characteristic other than 2, is called a linear reflection if 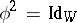 and if the rank of the transformation
and if the rank of the transformation 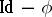 is equal to
is equal to 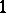 . In this case, the subspace
. In this case, the subspace  of fixed vectors relative to
of fixed vectors relative to  has codimension
has codimension  in
in  , the subspace
, the subspace 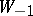 of eigenvectors with eigenvalue
of eigenvectors with eigenvalue 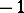 has dimension
has dimension 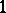 and
and 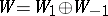 . If
. If 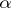 is a linear form on
is a linear form on  such that
such that 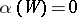 when
when 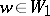 , and if
, and if 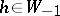 is an element such that
is an element such that 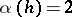 , then
, then  is defined by the formula
is defined by the formula
 |
The description of a reflection in an arbitrary simply-connected space 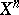 of constant curvature can be reduced to the description of linear reflections in the following way. Every such space
of constant curvature can be reduced to the description of linear reflections in the following way. Every such space  can be imbedded as a hypersurface in a real
can be imbedded as a hypersurface in a real 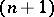 -dimensional vector space
-dimensional vector space  in such a way that the motions of
in such a way that the motions of 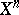 can be extended to linear transformations of
can be extended to linear transformations of 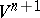 . Moreover, in a suitable coordinate system in
. Moreover, in a suitable coordinate system in 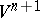 the equations of the hypersurface can be written in the following way:
the equations of the hypersurface can be written in the following way:
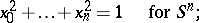 |
 |
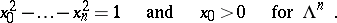 |
Every hypersurface in  , given this imbedding, is the intersection with
, given this imbedding, is the intersection with  of a certain
of a certain  -dimensional subspace in
-dimensional subspace in 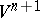 , and every reflection in
, and every reflection in 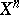 is induced by a linear reflection in
is induced by a linear reflection in 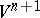 .
.
If, in the definition of a linear reflection, the requirement that  is dropped, then the more general concept of a pseudo-reflection is obtained. If
is dropped, then the more general concept of a pseudo-reflection is obtained. If 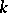 is the field of complex numbers and
is the field of complex numbers and 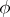 is a pseudo-reflection of finite order (not necessarily equal to 2), then
is a pseudo-reflection of finite order (not necessarily equal to 2), then 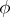 is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection.
is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection.
See also Reflection group.
References
| [1] | N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Hermann (1968) pp. Chapts. 4–6 |
| [2] | E.B. Vinberg, "Discrete linear groups generated by reflections" Math. USSR Izv. , 35 : 5 (1971) pp. 1083–1119 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 5 (1971) pp. 1072–1112 |
| [3] | E. Gottschling, "Reflections in bounded symmetric domains" Comm. Pure Appl. Math. , 22 (1969) pp. 693–714 |
| [4] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
The spelling reflexion also occurs in the literature.
A basic fact is that the reflections generate the orthogonal group; see [a2], Sects. 8.12.12, 13.7.12.
References
| [a1] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a2] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a3] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a4] | M. Greenberg, "Euclidean and non-euclidean geometry" , Freeman (1980) |
| [a5] | B. Artmann, "Lineare Algebra" , Birkhäuser (1986) |
| [a6] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) |
Reflection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reflection&oldid=15842