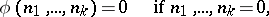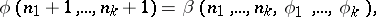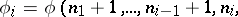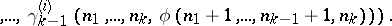A form of recursion using several variables simultaneously. The set of values of these variables is ordered lexicographically. This definition subsumes numerous concrete recursive descriptions. If in such a description the unknown function is not substituted into itself, then it results in a primitive recursion. In general, multiple recursion leads outside the limits of the set of primitive recursive functions, since by a double recursion (performed with respect to two variables) it is possible to construct a function which is universal for the primitive recursive functions (similarly, for 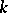 -recursive functions there is a
-recursive functions there is a 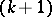 -multiple universal function); cf. Universal function. All possible forms of multiple recursion can be reduced to the following normal form:
-multiple universal function); cf. Universal function. All possible forms of multiple recursion can be reduced to the following normal form:
where
References
| [1] | R. Peter, "Recursive functions" , Acad. Press (1967) (Translated from German) |
It is more common to speak of simultaneous recursion, rather than multiple recursion; cf., e.g., [a1].
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [a2] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165 |
How to Cite This Entry:
Multiple recursion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiple_recursion&oldid=15829
This article was adapted from an original article by N.V. Belyakin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article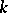 -recursive functions there is a
-recursive functions there is a 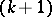 -multiple universal function); cf. Universal function. All possible forms of multiple recursion can be reduced to the following normal form:
-multiple universal function); cf. Universal function. All possible forms of multiple recursion can be reduced to the following normal form: