D'Alembert formula

A formula expressing the solution of the Cauchy problem for the wave equation with one spatial variable. Let the given functions , belong, respectively, to the spaces and , and let be continuous together with the first derivative with respect to in the half-plane . Then the classical solution in of the Cauchy problem

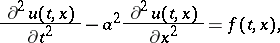(1)

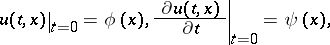(2)

is expressed by d'Alembert's formula:

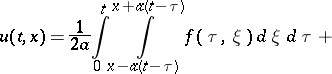If the functions 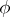and 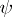are given and satisfy the above smoothness conditions on the interval 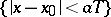, and if satisfies it in the triangle

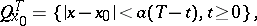then d'Alembert's formula gives the unique solution of the problem (1), (2) in 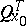. The requirements on the given functions may be weakened if one is interested in solutions in a certain generalized sense. For instance, it follows from d'Alembert's formula that if is integrable with respect to any triangle 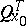, if is locally integrable and if 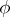is continuous, the weak solution of Cauchy's problem (1), (2) may be defined as a uniform limit (in any ) of classical solutions with smooth data and is also expressed by d'Alembert's formula.

The formula was named after J. d'Alembert (1747).

References

[1]	V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian)
[2]	A.N. Tikhonov, A.A. Samarskii, "Partial differential equations of mathematical physics" , 1–2 , Holden-Day (1976) (Translated from Russian)

References

[a1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)