Replica

of an algebraic system 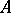in a given class 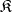of algebraic systems of the same signature

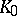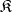An algebraic system from possessing the following properties: 1) there is a surjective homomorphis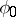m from 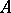onto ; 2) if 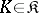and if 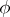is a homomorphism from 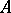to 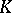, then 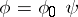for some homomorphism 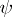from the system 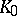to 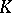. The replica of the system 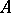in the class 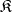(if it exists) is uniquely defined up to an isomorphism. The class 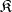is called replica full if it contains a replica for any algebraic system of the same signature. A class of algebraic systems of a fixed signature is replica full if and only if it contains a one-element system and is closed with respect to taking subsystems and direct products. The axiomatizable replica-full classes (and only these) are quasi-varieties (cf. Quasi-variety).

References

[1]	A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian)

Comments

The concept of a replica is closely related to that of a universal problem (cf. Universal problems).

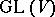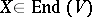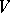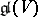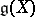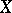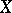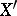A second notion of replica occurs in the theory of algebraic Lie algebras, the Lie algebras of algebraic subgroups of . Let , where is a finite-dimensional vector space, and let be the smallest algebraic Lie subalgebra of that contains . The elements of are called the replicas of . One has that is nilpotent if and only if for all replicas of .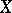

References

[a1]	C. Chevalley, "Théorie des groupes de Lie" , 2 , Hermann (1951) pp. Chapt. II, §14