Combinatorial geometry(2)

A finite set 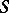together with a closure relation

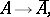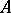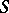defined for all subsets of (that is, 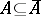, 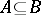implies 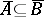and 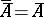, but not necessarily 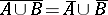), and satisfying the conditions: 1) for the empty set ; 2) 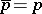for each element 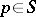; and 3) if 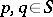and 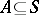and if 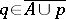but 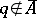, then 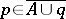(the "exchange" property). The closed sets, or subspaces, 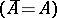form a geometric lattice (cf. Semi-Dedekind lattice). A subset 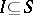is independent if 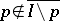for all 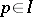; all maximal independent sets, or bases, have the same cardinality. The direct sum of combinatorial geometries and the restriction of a combinatorial geometry to a subset 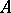are defined in the usual way. The cardinality of the bases of the restriction of a combinatorial geometry to 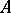is called the rank 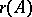of 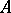. The rank function satisfies the condition

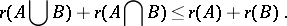A subset 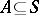for which 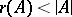is said to be dependent; the minimal dependent sets of a combinatorial geometry are called circuits. By dropping conditions 1) and 2) in the definition of a combinatorial geometry one obtains the definition of a pre-geometry or matroid. Infinite combinatorial geometries are also considered, but here it is required that the bases be finite.

Example of a combinatorial geometry. A subset 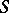of a vector space 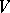with the relation

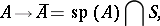defined for all 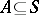, where 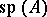is the linear subspace in 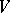spanned by .

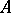One of the fundamental problems in the theory of combinatorial geometries is the so-called critical problem. For the combinatorial geometry defined by a set 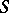in an -dimensional projective space over a Galois field, this problem consists in the determination of the smallest positive integer 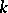(the critical exponent) for which there exists a family of hyperplanes 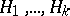distinguishing 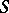. (A family of hyperplanes distinguishes a set 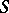if for every 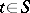there is at least one hyperplane not containing .)

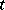References

[1]	H. Whitney, "On the abstract properties of linear dependence" Amer. J. Math. , 57 (1935) pp. 509–533
[2]	H.H. Crapo, G.C. Rota, "On the foundations of combinatorial theory: combinatorial geometries" , M.I.T. (1970)
[3]	W.T. Tutte, "Introduction to the theory of matroids" , American Elsevier (1971)
[4]	R.J. Wilson, "Introduction to graph theory" , Oliver & Boyd (1972)
[5]	K.A. Rybnikov, "Introduction to combinatorial analysis" , Moscow (1972) (In Russian)
[6]	D.J.A. Welsh, "Matroid theory" , Acad. Press (1976)
[7]	R. von Randow, "Introduction to the theory of matroids" , Springer (1975)
[8]	N. White (ed.) , Theory of matroids , Cambridge Univ. Press (1986)
[9]	K.A. Rybnikov (ed.) , Combinatorial analysis: exercises and problems , Moscow (1982) (In Russian)