Omega-completeness
From Encyclopedia of Mathematics
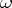 -completeness
-completeness
The property of formal systems of arithmetic in which, for any formula 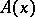 , from a deduction of
, from a deduction of 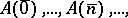 it follows that one can infer the formula
it follows that one can infer the formula 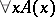 , where
, where 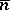 is a constant signifying the natural number
is a constant signifying the natural number  . If this is not true, the system is called
. If this is not true, the system is called 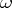 -incomplete. K. Gödel in his incompleteness theorem (cf. Gödel incompleteness theorem) actually established the
-incomplete. K. Gödel in his incompleteness theorem (cf. Gödel incompleteness theorem) actually established the 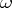 -incompleteness of formal arithmetic. If all formulas which are true in the standard model of arithmetic are taken as axioms, then an
-incompleteness of formal arithmetic. If all formulas which are true in the standard model of arithmetic are taken as axioms, then an 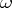 -complete axiom system is obtained. On the other hand, in every
-complete axiom system is obtained. On the other hand, in every 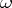 -complete extension of Peano arithmetic, every formula which is true in the standard model can be deduced.
-complete extension of Peano arithmetic, every formula which is true in the standard model can be deduced.
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
How to Cite This Entry:
Omega-completeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-completeness&oldid=15799
Omega-completeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-completeness&oldid=15799
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article