Group with unique division
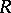 -group
-group
A group in which the equality 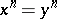 implies
implies 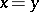 , where
, where 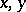 are any elements in the group and
are any elements in the group and  is any natural number. A group
is any natural number. A group 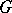 is an
is an  -group if and only if it is torsion-free and is such that
-group if and only if it is torsion-free and is such that 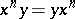 implies
implies  for any
for any 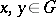 and any natural number
and any natural number  . An
. An 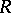 -group splits into the set-theoretic union of Abelian groups of rank 1 intersecting at the unit element. A group is an
-group splits into the set-theoretic union of Abelian groups of rank 1 intersecting at the unit element. A group is an  -group if and only if it is torsion-free and if its quotient group by the centre (cf. Centre of a group) is an
-group if and only if it is torsion-free and if its quotient group by the centre (cf. Centre of a group) is an 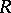 -group. Subgroups of an
-group. Subgroups of an 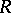 -group, as well as direct and complete direct products (cf. Direct product) of
-group, as well as direct and complete direct products (cf. Direct product) of 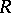 -groups, are
-groups, are 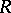 -groups. The following local theorem is valid for the class of
-groups. The following local theorem is valid for the class of 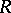 -groups: If all finitely-generated subgroups of a group
-groups: If all finitely-generated subgroups of a group 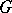 are
are 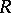 -groups, then
-groups, then 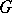 itself is an
itself is an 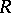 -group. Free groups, free solvable groups and torsion-free locally nilpotent groups (cf. Free group; Nilpotent group; Solvable group) are
-group. Free groups, free solvable groups and torsion-free locally nilpotent groups (cf. Free group; Nilpotent group; Solvable group) are 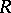 -groups. The class of all divisible
-groups. The class of all divisible 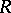 -groups (
-groups (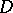 -groups, cf. also Divisible group) forms a variety of algebras under the operations of multiplication and division.
-groups, cf. also Divisible group) forms a variety of algebras under the operations of multiplication and division.
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
Group with unique division. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_with_unique_division&oldid=15786