Probability space
probability field
A triple 
consisting of a non-empty set 
, a class 
of subsets of 
which is a 
-algebra (i.e. is closed with respect to the set-theoretic operations executed a countable number of times) and a probability measure 
on 
. The concept of a probability space is due to A.N. Kolmogorov [1]. The points of 
are said to be elementary events, while the set 
itself is referred to as the space of elementary events or the sample space. The subsets of 
belonging to 
are (random) events. The study of probability spaces is often restricted to the study of complete probability spaces, i.e. spaces which satisfy the requirement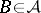 
, 
, 
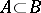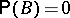implies 
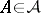. If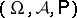 
is an arbitrary probability space, the class of sets of the type 
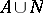, where 
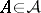and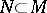 
, for some 
with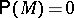 
, forms a 
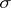-algebra 
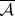, while the functi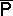on 
on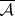 
defined by the formula 
is a probability measure on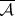 
. The space 
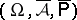is complete and is said to be the completion of 
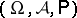. Usually one may restrict attention perfect probability spaces, i.e. spaces such that for any real 
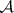-measurable function 
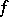and any set 
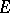on the real line for which 
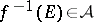, there exists a Borel set 
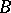such that 
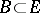and 
. Certain "pathological" effects (connected with the existence of conditional probabilities, the definition of independent random variables, etc.), which occur in the general scheme, cannot occur in perfect probability spaces. The problem of the existence of probability spaces satisfying some given special requirements is not trivial in many cases. One result of this type is the fundamental Kolmogorov consistency theorem: Let to each ordered 
-tuple 
of elements of a set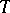 
correspond a probability measure 
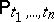on the Borel sets of the Euclidean space 
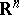and let the following consistency conditions be satisfied:
1) 
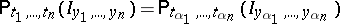for all 
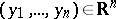, where 
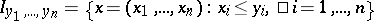and 
is an arbitrary rearrangement of the numbers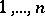 
;
2) 
.
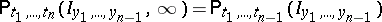Then there exists a probability measure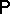 
on the smallest 
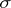-algebra 
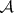of subsets of the product 
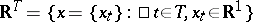with respect to which all the coordinate functions 
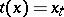are measurable, such that for any finite subset 
of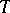 
and for any 
-dimensional Borel set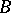 
the following equation is true:
 |
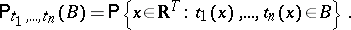References
| [1] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) |
| [2] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) |
| [3] | J. Neveu, "Mathematical foundations of the calculus of probabilities" , Holden-Day (1965) (Translated from French) |
Comments
References
| [a1] | P. Billingsley, "Probability and measure" , Wiley (1979) |
Probability space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Probability_space&oldid=15765