Bell-shaped game

A game on the unit square whose pay-off function takes the form 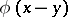, where 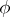is a positive analytic proper Pólya frequency function, i.e.:

1) 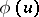is defined for all ;

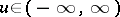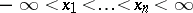2) for any and any sets and 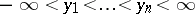there is an inequality ;

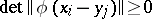3) for any set (correspondingly, 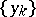) there is a set 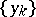(correspondingly, 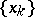) such that ;

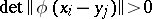4) .

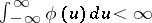An example of a bell-shaped game is a game with pay-off function 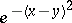. The optimal strategies of players in a bell-shaped game are unique and are piecewise-constant distributions with a finite number of steps. The value of a game with pay-off function 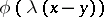, as , moves towards zero, while the number of points in the supports of the optimal strategies grows unboundedly.

References

[1]	S. Karlin, "Mathematical methods and theory in games, programming and economics" , Addison-Wesley (1959)