Sasakian manifold
Let 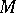 be a
be a 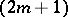 -dimensional differentiable manifold of class
-dimensional differentiable manifold of class 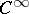 and let
and let 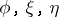 be a tensor field of type
be a tensor field of type 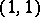 (cf. also Tensor on a vector space), a vector field and a
(cf. also Tensor on a vector space), a vector field and a 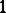 -form on
-form on 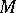 (cf. Differential form), respectively, such that
(cf. Differential form), respectively, such that
 |
where 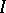 is the identity on the tangent bundle
is the identity on the tangent bundle 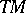 of
of 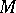 . Then
. Then 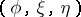 is said to be an almost contact structure on
is said to be an almost contact structure on 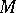 , and
, and 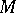 is called an almost contact manifold. If follows that
is called an almost contact manifold. If follows that
 |
and therefore 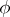 has the constant rank
has the constant rank 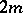 on
on 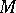 . Moreover, there exists a Riemannian metric
. Moreover, there exists a Riemannian metric 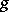 on
on 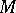 such that
such that
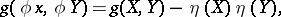 |
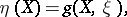 |
for any vector fields  ,
,  on
on 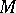 [a2]. Then
[a2]. Then 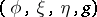 is said to be an almost contact metric structure and
is said to be an almost contact metric structure and 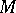 an almost contact metric manifold. On
an almost contact metric manifold. On 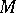 one defines the fundamental
one defines the fundamental  -form
-form 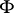 by
by
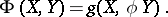 |
Then 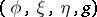 is said to be a contact metric structure on
is said to be a contact metric structure on 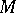 if
if 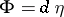 .
.
The Nijenhuis tensor field of  is the tensor field
is the tensor field 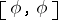 of type
of type 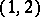 given by
given by
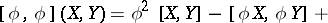 |
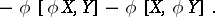 |
The almost contact structure  is said to be normal if
is said to be normal if
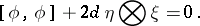 |
A manifold 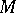 endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [a4]): An almost contact metric manifold
endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [a4]): An almost contact metric manifold 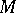 is Sasakian if and only if
is Sasakian if and only if
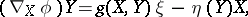 |
for any vector fields  ,
, 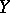 on
on 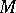 , where
, where  is the Levi-Civita connection on
is the Levi-Civita connection on 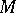 with respect to
with respect to 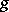 .
.
A plane section 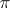 in
in 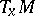 is called a
is called a 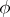 -section if there exists a unit vector
-section if there exists a unit vector 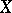 in
in 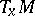 orthogonal to
orthogonal to  such that
such that 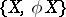 is an orthonormal basis of
is an orthonormal basis of 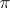 . The
. The 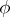 -sectional curvature of
-sectional curvature of 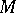 with respect to a
with respect to a 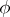 -section
-section 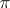 is defined by
is defined by 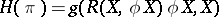 , where
, where 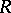 is the curvature tensor field of
is the curvature tensor field of  . When the
. When the 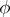 -sectional curvature does not depend on both the point
-sectional curvature does not depend on both the point 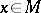 and the
and the 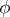 -section
-section 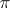 , one says that
, one says that 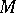 has constant
has constant 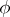 -sectional curvature and calls it a Sasakian space form.
-sectional curvature and calls it a Sasakian space form.
General references for Sasakian manifolds are [a2], [a3], [a6].
Submanifolds of Sasakian manifolds.
Three classes of submanifolds of a Sasakian manifold 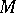 have been studied intensively.
have been studied intensively.
First, let 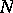 be a
be a 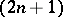 -dimensional submanifold of
-dimensional submanifold of 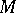 such that
such that  is tangent to
is tangent to  and
and  , for all
, for all 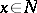 . Then
. Then  is said to be an invariant submanifold of
is said to be an invariant submanifold of 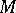 . It follows that
. It follows that 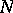 is a Sasakian manifold too, and, in general,
is a Sasakian manifold too, and, in general, 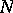 inherits the properties of the ambient Sasakian manifold
inherits the properties of the ambient Sasakian manifold 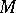 .
.
Next, an  -dimensional submanifold
-dimensional submanifold 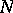 of
of 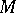 is an anti-invariant submanifold if
is an anti-invariant submanifold if  for all
for all 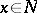 , where
, where 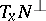 is the normal space of
is the normal space of 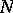 at
at  . The most important results on anti-invariant submanifolds have been collected in [a5].
. The most important results on anti-invariant submanifolds have been collected in [a5].
Finally, an  -dimensional submanifold
-dimensional submanifold 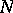 of
of 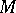 is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also CR-submanifold) if
is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also CR-submanifold) if 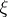 is tangent to
is tangent to  and there exist two distributions
and there exist two distributions 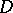 and
and 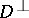 on
on 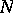 such that
such that 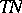 has the orthogonal decomposition
has the orthogonal decomposition 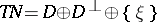 , with
, with 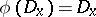 and
and 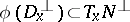 for all
for all 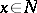 , where
, where 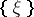 denotes the distribution spanned by
denotes the distribution spanned by 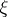 on
on 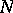 . For the geometry of semi-invariant submanifolds, see [a1].
. For the geometry of semi-invariant submanifolds, see [a1].
References
| [a1] | A. Bejancu, "Geometry of 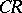 submanifolds" , Reidel (1986) submanifolds" , Reidel (1986) |
| [a2] | D.E. Blair, "Contact manifolds in Riemannian geometry" , Lecture Notes in Mathematics , 509 , Springer (1976) |
| [a3] | S. Sasaki, "Almost contact manifolds" , Lecture Notes , 1–3 , Math. Inst. Tôhoku Univ. (1965–1968) |
| [a4] | S. Sasaki, Y. Hatakeyama, "On differentiable manifolds with contact metric strctures" J. Math. Soc. Japan , 14 (1962) pp. 249–271 |
| [a5] | K. Yano, M. Kon, "Anti-invariant submanifolds" , M. Dekker (1976) |
| [a6] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
Sasakian manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sasakian_manifold&oldid=15719