Division
The operation inverse to multiplication: To find an  such that
such that  or
or  for given
for given  and
and  . The result
. The result  of the division is known as the quotient or the ratio between
of the division is known as the quotient or the ratio between  and
and  ;
;  is the divided, while
is the divided, while  is the divisor. The operation of division is denoted by a colon
is the divisor. The operation of division is denoted by a colon  , a horizontal stroke
, a horizontal stroke  or an oblique stroke
or an oblique stroke  .
.
In the field of rational numbers, division (except for division by zero) is always possible, and the result of a division is unique. In the ring of integers division is not always possible. Thus, 10 is divisible by 5, but is not divisible by 3. If the division of an integer  by an integer
by an integer  in the field of rational numbers yields a quotient which is also an integer, one says that
in the field of rational numbers yields a quotient which is also an integer, one says that  is totally divisible (divisible without remainder) by
is totally divisible (divisible without remainder) by  ; this is noted as
; this is noted as  . Division of complex numbers is defined by the formula
. Division of complex numbers is defined by the formula
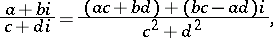 |
while division of the complex numbers in their trigonometric form is given by the formula
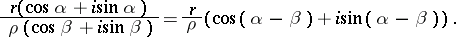 |
Division with remainder is actually a separate operation, which is different from division as defined above. If  and
and 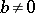 are integers, then division with remainder of
are integers, then division with remainder of  by
by 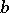 consists of finding integers
consists of finding integers  and
and 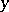 such that
such that
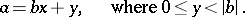 |
Here  is the divided,
is the divided,  is the divisor,
is the divisor,  is the quotient, and
is the quotient, and  is the remainder. This operation is always possible and is unique. If
is the remainder. This operation is always possible and is unique. If  , one says that
, one says that  divides
divides  without remainder. The quotient will then be the same as in ordinary division.
without remainder. The quotient will then be the same as in ordinary division.
Division with remainder of polynomials with coefficients in a given field is defined in a similar manner. It consists in finding, for two given polynomials  and
and  , polynomials
, polynomials  and
and  satisfying the conditions
satisfying the conditions
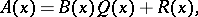 |
where the degree of  is less than that of
is less than that of  . This operation is also always possible and is unique. If
. This operation is also always possible and is unique. If  , one says that
, one says that 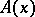 is divisible by
is divisible by  without remainder.
without remainder.
Comments
Division (with remainder) is related to the Euclidean algorithm.
Division of a complex number  by a complex number
by a complex number 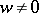 amounts to multiplying
amounts to multiplying  by
by 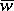 and dividing by
and dividing by  , i.e.
, i.e.
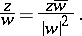 |
Here,  is the complex conjugate of
is the complex conjugate of 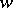 and
and  is the norm of
is the norm of  (cf. Complex number).
(cf. Complex number).
Division. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Division&oldid=15710