Excess coefficient
coefficient of excess, excess
A scalar characteristic of the pointedness of the graph of the probability density of a unimodal distribution. It is used as a certain measure of the deviation of the distribution in question from the normal one. The excess  is defined by the formula
is defined by the formula
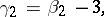 |
where  is the second Pearson coefficient (cf. Pearson distribution), and
is the second Pearson coefficient (cf. Pearson distribution), and  and
and  are the second and fourth central moments of the probability distribution. In terms of the second- and fourth-order semi-invariants (cumulants)
are the second and fourth central moments of the probability distribution. In terms of the second- and fourth-order semi-invariants (cumulants)  and
and  , the excess has the form
, the excess has the form
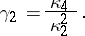 |
If  , then one says that the density of the probability distribution has normal excess, because for a normal distribution the excess is
, then one says that the density of the probability distribution has normal excess, because for a normal distribution the excess is 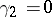 . When
. When 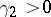 , one says that the probability distribution has positive excess, which corresponds, as a rule, to the fact that the graph of the density of the relevant distribution in a neighbourhood of the mode has a more pointed and higher vertex then a normal curve. When
, one says that the probability distribution has positive excess, which corresponds, as a rule, to the fact that the graph of the density of the relevant distribution in a neighbourhood of the mode has a more pointed and higher vertex then a normal curve. When 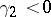 , one talks of a negative excess of the density, and then the probability density in a neighbourhood of the mode has a lower and flatter vertex than the density of a normal law.
, one talks of a negative excess of the density, and then the probability density in a neighbourhood of the mode has a lower and flatter vertex than the density of a normal law.
If 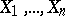 are independent random variables subject to one and same continuous probability law, then the statistic
are independent random variables subject to one and same continuous probability law, then the statistic
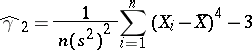 |
is called the sample excess, where
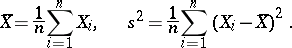 |
The sample excess 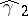 is used as a statistical point estimator of
is used as a statistical point estimator of 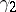 when the distribution law of the
when the distribution law of the 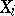 is not known. In the case of a normal distribution of the random variables
is not known. In the case of a normal distribution of the random variables 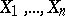 , the sample excess
, the sample excess 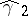 is asymptotically normally distributed, as
is asymptotically normally distributed, as 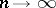 , with parameters
, with parameters
 |
and
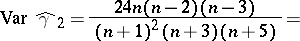 |
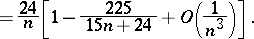 |
This is the reason why, when the observed value of 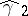 differs substantially from
differs substantially from  , one must assume that the distribution of the
, one must assume that the distribution of the 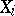 is not normal. This is used in practice to verify the hypothesis
is not normal. This is used in practice to verify the hypothesis 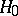 :
:  , which is equivalent to the fact that the distribution of the
, which is equivalent to the fact that the distribution of the 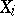 deviates from the normal distribution.
deviates from the normal distribution.
References
| [1] | M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , 3. Design and analysis , Griffin (1969) |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
The (coefficient of) excess is usually called the coefficient of kurtosis, or simply the kurtosis.
A density of normal, positive or negative excess is usually called a density of zero, positive or negative kurtosis, while a density of positive (negative) kurtosis is also said to be leptokurtic (respectively, platykurtic).
Excess coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Excess_coefficient&oldid=15672