Analytic ring
A ring of germs of analytic functions at a point in an analytic space. The following is a more accurate definition. Let 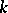 be a field with a non-trivial norm (cf. Norm on a field) (which is usually assumed to be complete), and let
be a field with a non-trivial norm (cf. Norm on a field) (which is usually assumed to be complete), and let 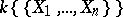 be the
be the 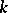 -algebra of power series in
-algebra of power series in 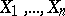 with coefficients in
with coefficients in 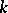 which converge on some polycylinder with centre
which converge on some polycylinder with centre 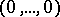 , each series converging on its own polycylinder. A quotient ring of the ring
, each series converging on its own polycylinder. A quotient ring of the ring 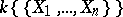 is called an analytic ring over
is called an analytic ring over 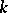 , or an analytic
, or an analytic 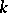 -algebra; usually,
-algebra; usually, 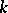 is the field of real numbers
is the field of real numbers 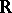 or the field of complex numbers
or the field of complex numbers 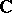 . Any analytic ring is a local, Noetherian, Hensel ring; its field of residues is isomorphic to
. Any analytic ring is a local, Noetherian, Hensel ring; its field of residues is isomorphic to 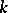 . An analytic ring
. An analytic ring 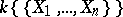 is a regular (and a factorial) ring, and its completion in the topology defined by the maximal ideal
is a regular (and a factorial) ring, and its completion in the topology defined by the maximal ideal 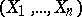 coincides with the ring of formal power series
coincides with the ring of formal power series 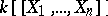 . The normalization lemma is true: An integral analytic ring is a finite extension of an analytic ring
. The normalization lemma is true: An integral analytic ring is a finite extension of an analytic ring  . Algebras that are finite over
. Algebras that are finite over 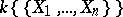 are generally called quasi-analytic
are generally called quasi-analytic 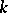 -algebras. If
-algebras. If 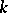 is a perfect field, an analytic ring is an excellent ring.
is a perfect field, an analytic ring is an excellent ring.
References
| [1] | J. Dieudonné, A. Grothendieck, "Critères differentiels de régularité pour les localisés des algèbres analytiques" J. of Algebra , 5 (1967) pp. 305–324 |
| [2] | B. Malgrange, "Ideals of differentiable functions" , Tata Inst. (1966) |
| [3] | S.S. Abhyankar, "Local analytic geometry" , Acad. Press (1964) |
Comments
References
| [a1] | H. Grauert, R. Remmert, "Coherent analytic sheaves" , Springer (1984) (Translated from German) |
Analytic ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_ring&oldid=15652