Dirichlet algebra
Let 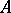 be a uniform algebra on
be a uniform algebra on 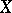 and
and 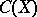 the algebra of all continuous functions on
the algebra of all continuous functions on 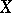 (cf. also Algebra of functions). The algebra
(cf. also Algebra of functions). The algebra 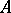 is called a Dirichlet algebra if
is called a Dirichlet algebra if 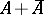 is uniformly dense in
is uniformly dense in 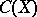 . Dirichlet algebras were introduced by A.M. Gleason [a4].
. Dirichlet algebras were introduced by A.M. Gleason [a4].
Let 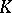 be a compact subset of the complex plane. Let
be a compact subset of the complex plane. Let 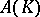 consist of those functions which are analytic on the interior of
consist of those functions which are analytic on the interior of 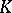 and let
and let 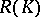 be the uniform closure in
be the uniform closure in 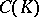 of the functions analytic on a neighbourhood of
of the functions analytic on a neighbourhood of 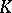 . T. Gamelin and J. Garnett [a3] determined exactly when
. T. Gamelin and J. Garnett [a3] determined exactly when 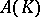 or
or 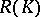 is a Dirichlet algebra on
is a Dirichlet algebra on 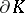 . The disc algebra
. The disc algebra 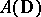 is the algebra of all functions which are analytic in the open unit disc
is the algebra of all functions which are analytic in the open unit disc 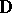 and continuous in the closed unit disc
and continuous in the closed unit disc 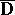 . The algebra
. The algebra 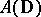 is a typical example of a Dirichlet algebra on the unit circle
is a typical example of a Dirichlet algebra on the unit circle 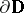 . For
. For 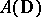 , the measure
, the measure
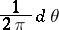 |
is the representing measure for the origin, that is,
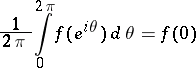 |
for 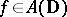 . The origin gives a complex homomorphism for
. The origin gives a complex homomorphism for 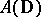 . For
. For 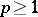 , the Hardy space
, the Hardy space 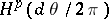 is defined as the closure of
is defined as the closure of 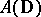 in
in 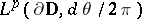 (cf. also Hardy spaces). Let
(cf. also Hardy spaces). Let 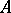 be a Dirichlet algebra on
be a Dirichlet algebra on 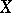 and
and 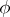 a non-zero complex homomorphism of
a non-zero complex homomorphism of 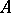 . If
. If 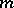 is a representing measure on
is a representing measure on 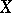 for
for 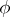 , then
, then 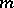 is unique. For
is unique. For 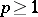 , the abstract Hardy space
, the abstract Hardy space 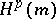 is defined as the closure of
is defined as the closure of 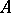 in
in 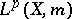 . A lot of theorems for the Hardy space
. A lot of theorems for the Hardy space 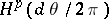 are valid for the abstract Hardy space
are valid for the abstract Hardy space 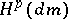 .
.
Let 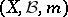 be a probability measure space (cf. also Probability measure; Measure space), let
be a probability measure space (cf. also Probability measure; Measure space), let 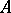 be a subalgebra of
be a subalgebra of 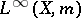 containing the constants and let
containing the constants and let 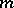 be multiplicative on
be multiplicative on 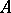 . The algebra
. The algebra 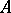 is called a weak
is called a weak Dirichlet algebra if
Dirichlet algebra if 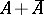 is weak
is weak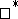 dense in
dense in 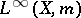 . A Dirichlet algebra is a weak
. A Dirichlet algebra is a weak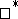 Dirichlet algebra when
Dirichlet algebra when 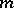 is a representing measure on it. Weak
is a representing measure on it. Weak Dirichlet algebras were introduced by T. Srinivasan and J. Wang [a9] as the smallest axiomatic setting on which each one of a lot of important theorems for the Hardy space
Dirichlet algebras were introduced by T. Srinivasan and J. Wang [a9] as the smallest axiomatic setting on which each one of a lot of important theorems for the Hardy space 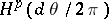 are equivalent to the fact that
are equivalent to the fact that 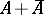 is weak
is weak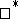 dense in
dense in  .
.
K. Hoffman and H. Rossi [a6] gave an example such that even if 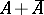 is dense in
is dense in 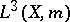 ,
, 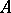 is not a weak
is not a weak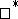 Dirichlet algebra. Subsequently, it was shown [a6] that if
Dirichlet algebra. Subsequently, it was shown [a6] that if 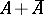 is dense in
is dense in 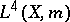 , then
, then 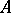 is a weak
is a weak Dirichlet algebra. W. Arveson [a1] introduced non-commutative weak
Dirichlet algebra. W. Arveson [a1] introduced non-commutative weak Dirichlet algebras, which are also called subdiagonal algebras.
Dirichlet algebras, which are also called subdiagonal algebras.
Examples of (weak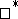 ) Dirichlet algebras.
) Dirichlet algebras.
Let 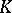 be a compact subset of the complex plane and suppose the algebra
be a compact subset of the complex plane and suppose the algebra 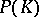 consists of the functions in
consists of the functions in 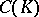 that can be approximated uniformly on
that can be approximated uniformly on 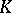 by polynomials in
by polynomials in  . Then
. Then 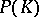 is a Dirichlet algebra on the outer boundary of
is a Dirichlet algebra on the outer boundary of 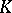 [a2].
[a2].
Let 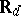 be the real line
be the real line 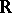 endowed with the discrete topology and suppose the algebra
endowed with the discrete topology and suppose the algebra 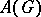 consists of the functions in
consists of the functions in 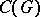 whose Fourier coefficients are zero on the semi-group
whose Fourier coefficients are zero on the semi-group 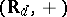 , where
, where 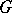 is the compact dual group of
is the compact dual group of 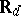 . Then
. Then 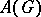 is a Dirichlet algebra on
is a Dirichlet algebra on 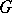 [a5].
[a5].
Let 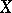 be a fixed compact Hausdorff space upon which the real line
be a fixed compact Hausdorff space upon which the real line  (with the usual topology) acts as a locally compact transformation group. The pair
(with the usual topology) acts as a locally compact transformation group. The pair 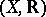 is called a flow. The translate of an
is called a flow. The translate of an 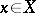 by a
by a 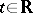 is written as
is written as 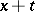 . A
. A 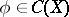 is called analytic if for each
is called analytic if for each 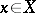 the function
the function 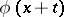 of
of 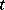 is a boundary function which is bounded and analytic in the upper half-plane. If
is a boundary function which is bounded and analytic in the upper half-plane. If 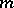 is an invariant ergodic probability measure on
is an invariant ergodic probability measure on 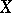 , then
, then 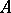 is a weak
is a weak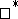 Dirichlet algebra in
Dirichlet algebra in 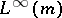 [a7]. See also Hypo-Dirichlet algebra.
[a7]. See also Hypo-Dirichlet algebra.
References
| [a1] | W. Arveson, "Analyticity in operator algebras" Amer. J. Math. , 89 (1967) pp. 578–642 |
| [a2] | H. Barbey, H. König, "Abstract analytic function theory and Hardy algebras" , Lecture Notes Math. : 593 , Springer (1977) |
| [a3] | T. Gamelin, J. Garnett, "Pointwise bounded approximation and Dirichlet algebras" J. Funct. Anal. , 8 (1971) pp. 360–404 |
| [a4] | A. Gleason, "Function algebras" , Sem. Analytic Functions , II , Inst. Adv. Study Princeton (1957) |
| [a5] | H. Helson, "Analyticity on compact Abelian groups" , Algebras in Analysis; Proc. Instructional Conf. and NATO Adv. Study Inst., Birmigham, 1973 , Acad. Press (1975) pp. 1–62 |
| [a6] | K. Hoffman, H. Rossi, "Function theory from a multiplicative linear functional" Trans. Amer. Math. Soc. , 102 (1962) pp. 507–544 |
| [a7] | P. Muhly, "Function algebras and flows" Acta Sci. Math. , 35 (1973) pp. 111–121 |
| [a8] | T. Nakazi, "Hardy spaces and Jensen measures" Trans. Amer. Math. Soc. , 274 (1982) pp. 375–378 |
| [a9] | T. Srinivasan, J. Wang, "Weak -Dirichlet algebras, Function algebras" , Scott Foresman (1966) pp. 216–249 -Dirichlet algebras, Function algebras" , Scott Foresman (1966) pp. 216–249 |
| [a10] | J. Wermer, "Dirichlet algebras" Duke Math. J. , 27 (1960) pp. 373–381 |
Dirichlet algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_algebra&oldid=15651