Osculation
of a curve  with a curve
with a curve 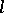 at a given point
at a given point 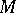
A geometrical concept, meaning that 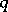 has contact of maximal order with
has contact of maximal order with  at
at  in comparison with any curve in some given family of curves
in comparison with any curve in some given family of curves 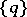 including
including 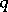 . The order of contact of
. The order of contact of  and
and  is said to be equal to
is said to be equal to  if the segment
if the segment 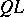 is a variable of
is a variable of 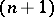 -st order of smallness with respect to
-st order of smallness with respect to 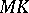 (see Fig., where
(see Fig., where  is perpendicular to the common tangent of
is perpendicular to the common tangent of 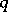 and
and 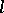 at
at 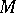 ).
).

Figure: o070590a
Thus, of all the curves in 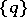 , the curve having osculation with
, the curve having osculation with 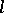 is the one which is most closely adjacent to
is the one which is most closely adjacent to 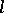 (that is, for which
(that is, for which 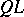 has maximal order of smallness). The curve in
has maximal order of smallness). The curve in 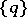 having osculation with
having osculation with 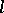 at a given point
at a given point 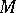 is called the osculating curve of the given family at this point. E.g., the osculating circle of
is called the osculating curve of the given family at this point. E.g., the osculating circle of  at
at 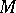 is the circle having maximal order of contact with
is the circle having maximal order of contact with 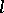 at
at 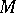 in comparison with any other circle.
in comparison with any other circle.
Similarly one can define the concept of osculation of a surface 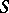 in a given family of surfaces
in a given family of surfaces 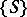 with a curve
with a curve 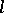 (or with a surface) at some point
(or with a surface) at some point 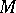 of it. Here the order of contact is defined similarly, except that one must examine the tangent plane of
of it. Here the order of contact is defined similarly, except that one must examine the tangent plane of 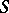 at
at 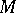 instead of the tangent line
instead of the tangent line 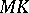 in the figure.
in the figure.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
| [2] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
| [3] | J. Favard, "Cours de géométrie différentielle locale" , Gauthier-Villars (1957) |
| [4] | V.A. Zalgaller, "The theory of envelopes" , Moscow (1975) (In Russian) |
Comments
The phrase "QL is a variable of the variable of n+1-st order of smallness with respect to another variablen+1-st order of smallness with respect to MK" means that 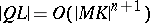 as
as  approaches
approaches  .
.
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1988) pp. Chapt. 2, Sect. 1.4 |
Osculation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculation&oldid=15619