Upper and lower bounds
Characteristics of sets on the real line. The least upper bound of a given set of real numbers is the smallest number bounding this set from above; its greatest lower bound is the largest number bounding it from below. This will now be restated in more detail. Let there be given a subset 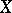 of the real numbers. A number
of the real numbers. A number 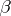 is said to be its least upper bound, denoted by
is said to be its least upper bound, denoted by 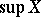 (from the Latin "supremum" — largest), if every number
(from the Latin "supremum" — largest), if every number 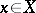 satisfies the inequality
satisfies the inequality 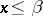 , and if for any
, and if for any 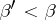 there exists an
there exists an 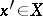 such that
such that 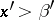 . A number
. A number 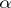 is said to be the greatest lower bound of
is said to be the greatest lower bound of 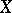 , denoted by
, denoted by 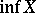 (from the Latin "infimum" — smallest), if every
(from the Latin "infimum" — smallest), if every 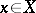 satisfies the inequality
satisfies the inequality 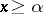 , and if for any
, and if for any 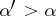 there exists an
there exists an 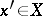 such that
such that 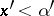 .
.
Examples.
 |
 |
if the set  consists of two points
consists of two points  and
and 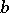 ,
, 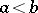 , then
, then
 |
These examples show, in particular, that the least upper bound (greatest lower bound) may either belong to the set (e.g. in the case of the interval 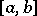 ) or not belong to it (e.g. in the case of the interval
) or not belong to it (e.g. in the case of the interval 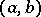 ). If a set has a largest (smallest) member, this number will clearly be the least upper bound (greatest lower bound) of the set.
). If a set has a largest (smallest) member, this number will clearly be the least upper bound (greatest lower bound) of the set.
The least upper bound (greatest lower bound) of a set not bounded from above (from below) is denoted by the symbol 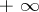 (respectively, by the symbol
(respectively, by the symbol 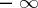 ). If
). If  is the set of natural numbers, then
is the set of natural numbers, then
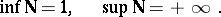 |
If  is the set of all integers, both positive and negative, then
is the set of all integers, both positive and negative, then
 |
Each non-empty set of real numbers has a unique least upper bound (greatest lower bound), finite or infinite. All non-empty sets bounded from above have finite least upper bounds, while all those bounded from below have finite greatest lower bounds.
The terms least upper (greatest lower) limit of a set are also sometimes used instead of the least upper bound (greatest lower bound) of a set, in one of the senses defined above. By the least upper bound (greatest lower bound) of a real-valued function, in particular of a sequence of real numbers, one means the least upper bound (greatest lower bound) of the set of its values (cf. also Upper and lower limits).
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1 , Moscow (1988) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
Commonly, an upper bound of a set 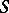 of real numbers is a number
of real numbers is a number 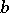 such that for all
such that for all 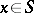 one has
one has 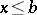 . The least upper bound of
. The least upper bound of 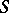 is then defined as an upper bound
is then defined as an upper bound 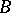 such that for every upper bound
such that for every upper bound 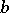 one has
one has 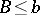 .
.
Analogous definitions hold for a lower bound and the greatest lower bound. If the least upper bound of 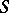 belongs to
belongs to 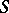 , then it is called the maximum of
, then it is called the maximum of 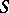 .
.
If the greatest lower bound of 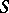 belongs to
belongs to 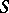 , then it is called the minimum of
, then it is called the minimum of 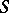 .
.
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
| [a3] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Upper and lower bounds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Upper_and_lower_bounds&oldid=15559