System of different representatives

system of distinct representatives, for a given family 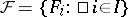of subsets of a set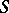

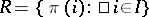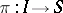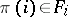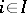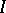A set determined by a one-to-one mapping that has the property: for any (here is an arbitrary index set). Another name for a system 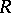of distinct representatives is transversal for the family 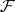. One also considers partial transversals of a family 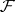, namely sets of the form 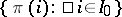, where 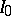is a subset of 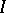and 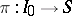is a one-to-one mapping.

Systems of distinct representatives are used both in purely combinatorial mathematical studies and in applications to linear programming, mathematical economics and cybernetics. In the framework of combinatorial mathematics, systems of distinct representatives play an important role in questions of choice and in extremal problems. They are used, in particular, in the study of Latin squares, in the assignment problem, in various extremal problems, in min-max theorems, and in the study of matrices with non-negative entries and with row and column sums in given ranges.

A criterion for the existence of a system of distinct representatives for a finite set 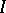is given by Phillip Hall's theorem: On a set 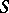, let a family 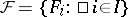of 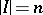elements, finite, be given; a system of distinct representatives exists if and only if 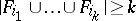for every 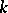-subset 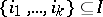and for every 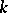, 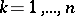. Hall's theorem is equivalent to König's theorem (see Selection theorems) about matrices of zeros and ones. This fundamental criterion can also be applied to infinite sets 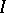when all 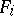, , 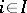are finite. Roughly speaking, as is shown by examples, such cases exhaust the domain of applicability of Hall's criterion, but it serves as a starting point for various criteria in several other cases (see [3]). For example: a) when there is a subset 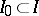for which 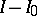is finite and the 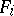are finite for all 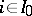; or b) when 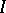is a countable set.

In view of the wide use of systems of distinct representatives, algorithms for their practical determination (see [1]) are of interest.

One of the main problems on systems of distinct representatives is the problem of the number of such systems for finite families of finite sets; this is connected with the calculation of the permanent of a matrix of zeros and ones. There are lower bounds for the number of such systems. Let the family 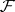consist of subsets 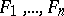and let these be ordered by cardinality: 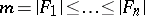. If 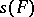satisfies Hall's criterion, then the number of systems of distinct representatives is at least

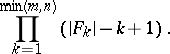Questions on systems of representatives are dealt with also in the theory of matroids (cf. Matroid, also called independence spaces or combinatorial geometries, cf. Combinatorial geometry). The connection between the theory of representatives and matroids is given by the Edmonds–Fulkerson theorem: For a given family of subsets of a finite set, the totality of all partial transversals is the totality of independent subsets of some matroid. The matroid so obtained from the family 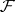is called the transversal matroid for 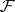. Many matroids can be represented as transversal matroids for some family of sets.

The concept of a system of distinct representatives can be generalized in various directions, for example: a) 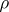-transversals for a given family 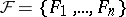and an integral vector 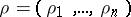are sets 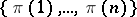, where the 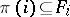, , 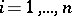are pairwise disjoint subsets of 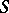such that 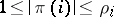; b) 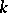-transversals for 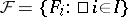and an integer 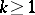are subsets 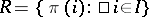for mappings 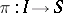with the properties 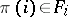and , .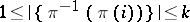

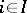References

[1]	M. Hall, "Combinatorial theory" , Wiley (1986)
[2]	L. Mirsky, "Transversal theory" , Acad. Press (1971)
[3]	V.E. Tarakanov, "On systems of representatives" , Problems of Cybernetics , 16 , Moscow (1975) pp. 110–124 (In Russian)

References

[a1]	H.J. Ryser, "Combinatorial mathematics" , Math. Assoc. Amer. (1963)
[a2]	D.J.A. Welsh, "Matroid theory" , Acad. Press (1976)
[a3]	M. Aigner, "Combinatorial theory" , Springer (1979) pp. Chapt. II (Translated from German)