The representation of a ring as the direct sum of subrings related to a given idempotent  . For a ring
. For a ring  containing an idempotent
containing an idempotent  , there exist left, right and two-sided Peirce decompositions, which are defined by
, there exist left, right and two-sided Peirce decompositions, which are defined by
respectively. If  has no identity, then one puts, by definition,
has no identity, then one puts, by definition,
The sets 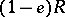 and
and 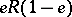 are defined analogously. Therefore, in a two-sided Peirce decomposition an element
are defined analogously. Therefore, in a two-sided Peirce decomposition an element 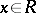 can be represented as
can be represented as
in a left decomposition as
and in a right decomposition as
There is also a Peirce decomposition with respect to an orthogonal system of idempotents 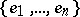 where
where 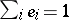 :
:
This decomposition was proposed by B. Peirce [1].
References
| [1] | B. Peirce, "Linear associative algebra" Amer. J. Math. , 4 (1881) pp. 97–229 |
In modern ring theory the Peirce decomposition appears in the ring of a Morita context 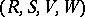 , where
, where  and
and 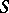 are Morita related if they are subrings of a ring
are Morita related if they are subrings of a ring  with an idempotent
with an idempotent  such that
such that 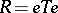 ,
, 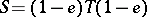 , i.e., they are parts of a Peirce decomposition of
, i.e., they are parts of a Peirce decomposition of 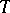 (see [a3], p.12).
(see [a3], p.12).
A context or a set of pre-equivalence data is a sextuple  where
where 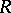 and
and  are rings,
are rings, 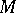 is a left
is a left  -, right
-, right 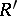 -bimodule,
-bimodule,  is a right
is a right 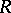 -, left
-, left 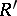 -bimodule and
-bimodule and 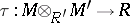 ,
, 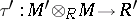 are bimodule homomorphisms, such that the following two associativity diagrams commute:
are bimodule homomorphisms, such that the following two associativity diagrams commute:
and
Using  , the set of all
, the set of all 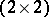 -matrices
-matrices
acquires a multiplication (using the usual matrix formulas) and this multiplication is associative precisely if the two diagrams above commute. Such a ring is then called the ring of a Morita context.
If  is a Morita context with
is a Morita context with  and
and 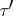 epic, then the functors
epic, then the functors 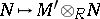 ,
, 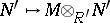 define an equivalence of categories between the categories of left
define an equivalence of categories between the categories of left  -modules and right
-modules and right  -modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.
-modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.
References
| [a1] | L.H. Rowen, "Ring theory" , I , Acad. Press (1988) pp. 36 |
| [a2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) pp. 48, 50 |
| [a3] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) |
How to Cite This Entry:
Peirce decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Peirce_decomposition&oldid=15535
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article . For a ring
. For a ring  containing an idempotent
containing an idempotent  , there exist left, right and two-sided Peirce decompositions, which are defined by
, there exist left, right and two-sided Peirce decompositions, which are defined by
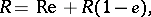
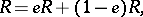
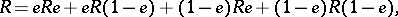
 has no identity, then one puts, by definition,
has no identity, then one puts, by definition,
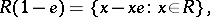
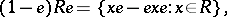
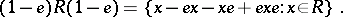
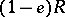 and
and 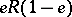 are defined analogously. Therefore, in a two-sided Peirce decomposition an element
are defined analogously. Therefore, in a two-sided Peirce decomposition an element 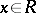 can be represented as
can be represented as
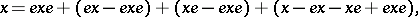
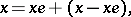
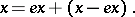
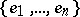 where
where 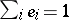 :
:
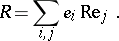
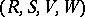 , where
, where  and
and 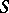 are Morita related if they are subrings of a ring
are Morita related if they are subrings of a ring  with an idempotent
with an idempotent  such that
such that 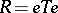 ,
, 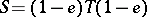 , i.e., they are parts of a Peirce decomposition of
, i.e., they are parts of a Peirce decomposition of 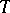 (see [a3], p.12).
(see [a3], p.12).
 where
where 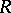 and
and  are rings,
are rings, 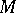 is a left
is a left  -, right
-, right 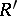 -bimodule,
-bimodule,  is a right
is a right 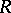 -, left
-, left 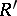 -bimodule and
-bimodule and 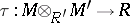 ,
, 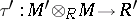 are bimodule homomorphisms, such that the following two associativity diagrams commute:
are bimodule homomorphisms, such that the following two associativity diagrams commute:
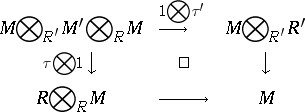
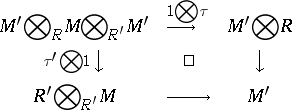
 , the set of all
, the set of all 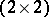 -matrices
-matrices
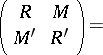
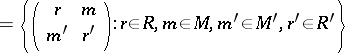
 is a Morita context with
is a Morita context with  and
and 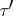 epic, then the functors
epic, then the functors 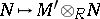 ,
, 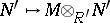 define an equivalence of categories between the categories of left
define an equivalence of categories between the categories of left  -modules and right
-modules and right  -modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.
-modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.