Chebyshev inequality
From Encyclopedia of Mathematics
for finite monotone sequences
 |
The inequality
 |
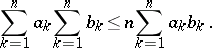Chebyshev's inequality for monotone functions 
is the inequality
 |
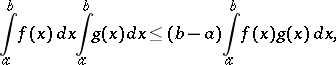where 
and 
are either both increasing or both decreasing on 
.
The inequalities were established by P.L. Chebyshev in 1882.
Comments
It is not important that 
and 
be non-negative. The proof consists of simply integrating the non-negative function 
over the square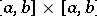 
.
How to Cite This Entry:
Chebyshev inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_inequality&oldid=15534
Chebyshev inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_inequality&oldid=15534
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article