Quantum groups
The phrase "quantum group" is more or less a synonym for "Hopf algebra" . More precisely, the category of quantum groups is defined in [a1] to be dual to the category of Hopf algebras. This is natural for the following reason. There is the following general principle: The functor 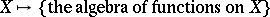 is an anti-equivalence between the category of "spaces" and the category of commutative associative unital algebras, perhaps with some additional structures or properties (this principle becomes a theorem if "space" is understood to be "affine scheme" or "compact topological space" , and "algebra" is understood to mean "C*-algebra" ). So one can translate the definition of a group into the language of algebras: instead of a space
is an anti-equivalence between the category of "spaces" and the category of commutative associative unital algebras, perhaps with some additional structures or properties (this principle becomes a theorem if "space" is understood to be "affine scheme" or "compact topological space" , and "algebra" is understood to mean "C*-algebra" ). So one can translate the definition of a group into the language of algebras: instead of a space 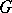 with an associative operation
with an associative operation 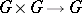 one obtains a commutative algebra
one obtains a commutative algebra 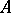 over a commutative ring
over a commutative ring 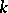 with a homomorphism
with a homomorphism 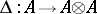 , called comultiplication; the unit
, called comultiplication; the unit 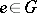 gives rise to a homomorphism
gives rise to a homomorphism 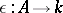 , called co-unit, and the mapping
, called co-unit, and the mapping 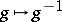 ,
, 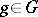 , gives rise to a bijective
, gives rise to a bijective 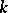 -linear mapping
-linear mapping 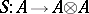 , called antipode. The group axioms are equivalent to the commutativity of the following diagrams:
, called antipode. The group axioms are equivalent to the commutativity of the following diagrams:
 |
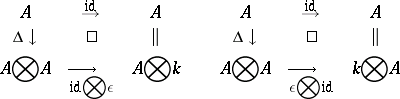 |
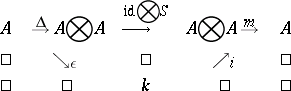 |
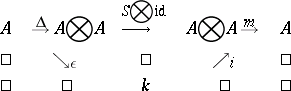 |
Here 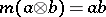 ,
, 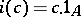 . The commutativity of these diagrams means that
. The commutativity of these diagrams means that 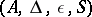 is a commutative Hopf algebra. Since the category of groups is anti-equivalent to the category of commutative Hopf algebras, it is natural to define a quantum group as an object of the category dual to the category of (not necessarily commutative) Hopf algebras.
is a commutative Hopf algebra. Since the category of groups is anti-equivalent to the category of commutative Hopf algebras, it is natural to define a quantum group as an object of the category dual to the category of (not necessarily commutative) Hopf algebras.
A simple class of non-commutative Hopf algebras is formed by the group algebras of non-commutative groups. These Hopf algebras are commutative, i.e.  is contained in the symmetric part of
is contained in the symmetric part of  . Essentially, all cocommutative Hopf algebras are group algebras.
. Essentially, all cocommutative Hopf algebras are group algebras.
Here is an example of a Hopf algebra which is neither commutative nor cocommutative. Fix 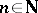 and
and  , where
, where 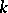 is a commutative ring. Denote by
is a commutative ring. Denote by 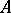 the associative
the associative 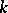 -algebra with generators
-algebra with generators 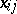 ,
, 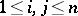 , and defining relations
, and defining relations 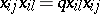 if
if 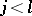 ,
, 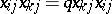 if
if 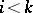 ,
,  if
if 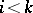 ,
, 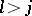 ,
, 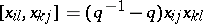 if
if 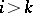 ,
, 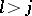 ,
,  , where
, where 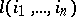 is the number of inversions in the permutation
is the number of inversions in the permutation  . Then
. Then 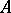 has a Hopf algebra structure defined by
has a Hopf algebra structure defined by 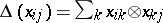 . If
. If 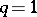 , then
, then  is the algebra of polynomial functions on
is the algebra of polynomial functions on 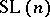 . So, in the general case it is natural to consider elements of
. So, in the general case it is natural to consider elements of 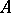 as "functions on the quantized SLn" .
as "functions on the quantized SLn" .
The quantized 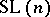 is one of the simplest quantum groups which appear naturally in the theory of quantum integrable systems and, especially, in the quantum inverse-scattering method [a2]. The development of this method has led to the following quantization technique for constructing non-commutative non-cocommutative Hopf algebras. It is natural to construct them as deformations of commutative Hopf algebras. If a non-commutative deformation
is one of the simplest quantum groups which appear naturally in the theory of quantum integrable systems and, especially, in the quantum inverse-scattering method [a2]. The development of this method has led to the following quantization technique for constructing non-commutative non-cocommutative Hopf algebras. It is natural to construct them as deformations of commutative Hopf algebras. If a non-commutative deformation 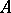 of a commutative Hopf algebra
of a commutative Hopf algebra 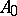 is given, then a Poisson bracket on
is given, then a Poisson bracket on 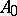 is defined by
is defined by 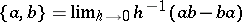 , where
, where 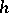 is the deformation parameter and
is the deformation parameter and 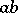 means the deformed product, which is not commutative. This Poisson bracket has the usual properties (skew-symmetry, Jacobi identity,
means the deformed product, which is not commutative. This Poisson bracket has the usual properties (skew-symmetry, Jacobi identity, 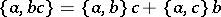 ) and is compatible with comultiplication. In other words,
) and is compatible with comultiplication. In other words,  is a Poisson–Hopf algebra. Therefore it is natural to start with a Poisson–Hopf algebra
is a Poisson–Hopf algebra. Therefore it is natural to start with a Poisson–Hopf algebra 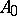 and then try to quantize it, i.e. to construct a Hopf algebra deformation of
and then try to quantize it, i.e. to construct a Hopf algebra deformation of 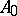 which induces the given Poisson bracket on
which induces the given Poisson bracket on  .
.
Technically it is more convenient to deform not commutative Hopf algebras but cocommutative ones and to start not with a Poisson–Hopf algebra (or a Poisson–Lie group [a1], which is more or less the same) but with its infinitesimal version, called a Lie bi-algebra . A Lie bi-algebra is a Lie algebra  with a linear mapping
with a linear mapping 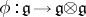 such that: 1)
such that: 1) 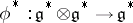 defines a Lie algebra structure on
defines a Lie algebra structure on 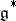 ; and 2)
; and 2)  is a
is a 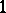 -cocycle (
-cocycle (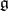 acts on
acts on 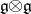 by means of the adjoint representation). By definition, a quantization of
by means of the adjoint representation). By definition, a quantization of 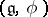 is a Hopf algebra deformation of the universal enveloping algebra
is a Hopf algebra deformation of the universal enveloping algebra  such that
such that 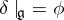 , where
, where 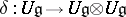 is the Poisson cobracket, defined by
is the Poisson cobracket, defined by 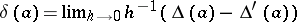 . Here
. Here 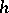 is the deformation parameter,
is the deformation parameter,  the deformed comultiplication and
the deformed comultiplication and 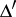 the opposite comultiplication.
the opposite comultiplication.
It is not known whether every Lie bi-algebra can be quantized, and usually quantization is not unique. But in several important cases (cf. [a1], §3, §6) there exists a canonical quantization. In particular, on a Kac–Moody algebra 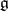 with a fixed scalar product
with a fixed scalar product  there is a canonical Lie bi-algebra structure and this bi-algebra has a canonical quantization
there is a canonical Lie bi-algebra structure and this bi-algebra has a canonical quantization 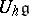 , as was discovered in [a3], [a4], [a5]. Let
, as was discovered in [a3], [a4], [a5]. Let 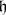 be the Cartan subalgebra of
be the Cartan subalgebra of 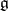 ,
, 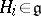 the images of the simple roots
the images of the simple roots 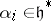 . Then
. Then 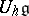 is generated by
is generated by 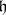 and
and 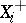 ,
, 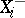 with the following defining relations:
with the following defining relations:
 |
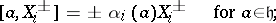 |
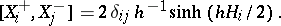 |
Setting 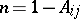 ,
, 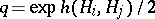 one has also
one has also
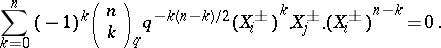 |
Here 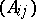 is the Cartan matrix and
is the Cartan matrix and 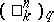 is the Gauss polynomial, i.e.,
is the Gauss polynomial, i.e.,
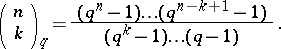 |
The comultiplication in  is such that
is such that 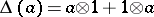 for
for 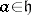 and
and
 |
If 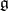 is a finite-dimensional simple Lie algebra (cf. Lie algebra, semi-simple), then the algebra of regular functions on the corresponding simply-connected algebraic group
is a finite-dimensional simple Lie algebra (cf. Lie algebra, semi-simple), then the algebra of regular functions on the corresponding simply-connected algebraic group  is isomorphic to the subalgebra of
is isomorphic to the subalgebra of 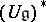 generated by the matrix elements of the finite-dimensional representations of
generated by the matrix elements of the finite-dimensional representations of 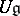 . Therefore the subalgebra of
. Therefore the subalgebra of 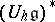 generated by the matrix elements of the finite-dimensional representations of
generated by the matrix elements of the finite-dimensional representations of 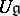 can be considered as the algebra of functions on a certain quantization of
can be considered as the algebra of functions on a certain quantization of 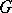 . For instance, the quantized
. For instance, the quantized 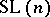 (cf. above) can be obtained in this way.
(cf. above) can be obtained in this way.
There is an important notion of a quasitriangular Hopf algebra. This is a pair 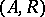 where
where  is a Hopf algebra and
is a Hopf algebra and 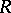 is an invertible element of
is an invertible element of 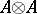 such that
such that 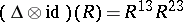 ,
, 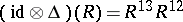 ,
, 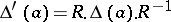 for
for 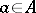 . Here
. Here  is the opposite comultiplication and
is the opposite comultiplication and 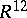 ,
, 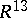 ,
, 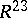 are defined as follows: If
are defined as follows: If 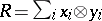 , where
, where 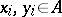 , then
, then 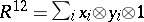 ,
, 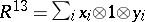 ,
, 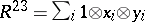 . If
. If 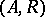 is a quasitriangular Hopf algebra, then
is a quasitriangular Hopf algebra, then 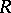 satisfies the quantum Yang–Baxter equation (cf. also Yang–Baxter equation), i.e.,
satisfies the quantum Yang–Baxter equation (cf. also Yang–Baxter equation), i.e., 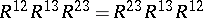 . It is known (cf. [a1], §13) that if
. It is known (cf. [a1], §13) that if 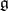 is a finite-dimensional simple Lie algebra, then
is a finite-dimensional simple Lie algebra, then 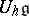 has a canonical quasitriangular structure, while if
has a canonical quasitriangular structure, while if 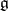 is an infinite-dimensional Kac–Moody algebra, then
is an infinite-dimensional Kac–Moody algebra, then 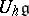 has an "almost quasitriangular" structure.
has an "almost quasitriangular" structure.
If 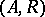 is a quasitriangular Hopf algebra over
is a quasitriangular Hopf algebra over 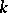 and
and 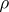 is a representation
is a representation 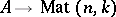 , then
, then 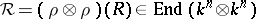 satisfies the quantum Yang–Baxter equation. There is an inverse construction (cf. [a6], [a7]), which goes back to the quantum inverse-scattering method: to a matrix solution of the quantum Yang–Baxter equation satisfying a non-degeneracy condition there corresponds a Hopf algebra. Without this condition one can only construct an associative bi-algebra (the difference between a Hopf algebra and an associative bi-algebra is that in the second case there may be no antipode). This bi-algebra is generated by elements
satisfies the quantum Yang–Baxter equation. There is an inverse construction (cf. [a6], [a7]), which goes back to the quantum inverse-scattering method: to a matrix solution of the quantum Yang–Baxter equation satisfying a non-degeneracy condition there corresponds a Hopf algebra. Without this condition one can only construct an associative bi-algebra (the difference between a Hopf algebra and an associative bi-algebra is that in the second case there may be no antipode). This bi-algebra is generated by elements 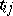 ,
, 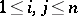 , with defining relations
, with defining relations 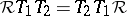 , where
, where 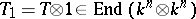 ,
, 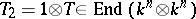 ,
, 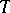 is the matrix
is the matrix 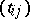 , and
, and 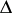 is defined by
is defined by 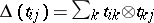 .
.
Quasitriangular Hopf algebras are a natural tool for the quantum inverse-scattering in method ([a1], §11). On the other hand, they can be used (cf. [a8]) to construct invariants of knots (and of more general objects such as links and tangles) generalizing the Jones polynomial [a9]. More precisely, to an oriented knot 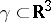 and a quasitriangular Hopf algebra
and a quasitriangular Hopf algebra  there corresponds a central element
there corresponds a central element 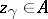 .
.
The usual notion of a group has several versions: abstract group, Lie group, topological group, etc. The same is true for quantum groups. The quantum analogue of the notion of a compact group was introduced in [a10] (the idea is to use 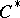 -algebras instead of abstract algebras). The quantized
-algebras instead of abstract algebras). The quantized 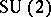 (cf. [a11], [a12]) is a typical example. The notion of a ring group (cf. , [a14]) and the equivalent notion of a Kac algebra (cf. [a15], [a16]) were introduced as an attempt to define a locally compact quantum group. However, these notions are not general enough (the axioms of , [a14], [a15] imply that the square of the antipode is the identity mapping, and therefore the quantized
(cf. [a11], [a12]) is a typical example. The notion of a ring group (cf. , [a14]) and the equivalent notion of a Kac algebra (cf. [a15], [a16]) were introduced as an attempt to define a locally compact quantum group. However, these notions are not general enough (the axioms of , [a14], [a15] imply that the square of the antipode is the identity mapping, and therefore the quantized 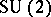 is not a ring group).
is not a ring group).
References
| [a1] | V.G. Drinfel'd, "Quantum groups" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 798–820 |
| [a2] | L.D. Faddeev, "Integrable models in (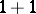 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1984) pp. 563–608 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1984) pp. 563–608 |
| [a3] | M. Jimbo, "Quantum 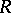 -matrix for the generalized Toda system" Comm. Math. Phys. , 102 (1986) pp. 537–547 -matrix for the generalized Toda system" Comm. Math. Phys. , 102 (1986) pp. 537–547 |
| [a4] | M. Jimbo, "A 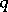 -difference analogue of -difference analogue of 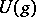 and the Yang–Baxter equation" Letters Math. Phys. , 10 (1985) pp. 63–69 and the Yang–Baxter equation" Letters Math. Phys. , 10 (1985) pp. 63–69 |
| [a5] | V.G. Drinfel'd, "Hopf algebras and the quantum Yang–Baxter equation" Soviet Math. Dokl. , 32 (1985) pp. 254–258 Dokl. Akad. Nauk SSSR , 283 : 5 (1985) pp. 1060–1064 |
| [a6] | V.V. Lyubashenko, "Hopf algebras and vector symmetries" Russian Math. Surveys , 41 : 5 (1986) pp. 153–154 Uspekhi Mat. Nauk , 41 : 5 (1986) pp. 185–186 |
| [a7] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtayan, "Quantization of Lie groups and Lie algebras" Algebra and Analysis , 1 : 1 (1989) pp. 178–206 (In Russian) |
| [a8] | N.Yu. Reshetikhin, "Quasitriangular Hopf algebras and invariants of tangles" Algebra and Analysis , 1 : 2 (1989) pp. 169–188 (In Russian) |
| [a9] | V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" Bulletin Amer. Math. Soc. , 12 (1985) pp. 103–112 |
| [a10] | S.L. Woronowich, "Compact matrix pseudogroups" Comm. Math. Phys. , 111 (1987) pp. 613–665 |
| [a11] | S.L. Woronowich, "Twisted SU(2) group. An example of a noncommutative differential calculus" Publ. RIMS , 23 (1987) pp. 117–181 |
| [a12] | L.L. Vaksman, Ya.S. Soibelman, "Function algebra on the quantum group SU(2)" Funct. Anal. Appl. , 22 : 3 (1988) pp. 170–181 Funksional. Anal. Prilozhen. , 22 : 3 (1988) pp. 1–14 |
| [a13a] | G.I. Kac, "Ring groups and the duality principle I" Trans. Moscow Math. Soc. , 12 (1963) pp. 291–339 Trudy Moskov. Mat. Obshch. , 12 (1963) pp. 295–301 |
| [a13b] | G.I. Kac, "Ring groups and the duality principle II" Trans. Moscow Math. Soc. , 13 (1965) pp. 94–126 Trudy Moskov. Mat. Obshch. , 13 (1965) pp. 84–113 |
| [a14] | G.I. Kac, L.I. Vainerman, "Nonunimodular ring groups and Hopf–von Neumann algebras" Math. USSR Sb. , 23 (1974) pp. 185–214 Mat. Sb. , 94 : 2 (1974) pp. 194–225; 335 |
| [a15] | M. Enock, J.-M. Schwartz, "Une dualité dans les algèbres de von Neumann" Bull. Soc. Math. France , 44 (1975) pp. 1–44 |
| [a16] | J.-M. Schwartz, "Relations entre "ring groups" et algèbres de Kac" Bull. Sci. Math. (2) , 100 (1976) pp. 289–300 |
Quantum groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_groups&oldid=15533