Deformation over a principal base
A deformation 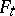 of a surface
of a surface 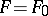 under which the directions of extremal deformation remain unaltered. The net formed by the curves which have the direction of extremal deformation is conjugate on each surface
under which the directions of extremal deformation remain unaltered. The net formed by the curves which have the direction of extremal deformation is conjugate on each surface  and is called the principal base of the deformation. For example, a helicoid has an infinite number of principal bases; surfaces of rotation and general canal surfaces allow a deformation over a principal base with geodesics as one family (see also Voss surface). The problem of investigating a deformation over a principal base was posed by K.M. Peterson [1]; in 1866 he established that if a surface
and is called the principal base of the deformation. For example, a helicoid has an infinite number of principal bases; surfaces of rotation and general canal surfaces allow a deformation over a principal base with geodesics as one family (see also Voss surface). The problem of investigating a deformation over a principal base was posed by K.M. Peterson [1]; in 1866 he established that if a surface 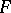 is isometrically transformed into two surfaces
is isometrically transformed into two surfaces 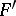 and
and  such that the directions of extremal deformation (and consequently, the base of the deformation, cf. Base of a deformation) from
such that the directions of extremal deformation (and consequently, the base of the deformation, cf. Base of a deformation) from 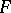 to
to 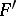 coincide with the directions of extremal deformation of
coincide with the directions of extremal deformation of 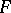 to
to  , then a deformation
, then a deformation 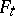 of the surface
of the surface  exists which includes
exists which includes  and
and  , with the same directions of extremal deformation. In other words, if a conjugate net on
, with the same directions of extremal deformation. In other words, if a conjugate net on 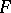 serves as the base of two different deformations
serves as the base of two different deformations 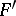 and
and  , then it is a principal base of deformation.
, then it is a principal base of deformation.
If the surfaces 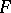 ,
, 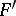 and
and 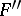 are known, then all remaining surfaces
are known, then all remaining surfaces 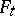 obtainable by deforming
obtainable by deforming 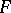 over a principal base are determined by the following theorem: Let
over a principal base are determined by the following theorem: Let 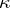 be the normal curvature of
be the normal curvature of 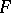 in the direction of one of the two families of the principal base
in the direction of one of the two families of the principal base 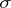 at an arbitrary point
at an arbitrary point  , while
, while  ,
,  ,
,  are the normal curvatures of the surfaces
are the normal curvatures of the surfaces 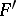 ,
, 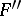 and
and 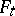 at the corresponding points and in the corresponding directions, then the cross ratio
at the corresponding points and in the corresponding directions, then the cross ratio 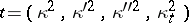 is a constant quantity for all positions of
is a constant quantity for all positions of 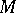 on
on  .
.
A surface which allows a deformation over a principal base can be characterized by only the spherical image of the principal base: The equations which describe a deformation over a principal base are transformed so as to contain only the coefficients of the line element of the spherical image of the surface and take the form:  (Kosser's equation), where
(Kosser's equation), where 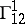 ,
,  are the Christoffel symbols of the third fundamental form of the surface, while the differentiation takes place along the coordinate lines
are the Christoffel symbols of the third fundamental form of the surface, while the differentiation takes place along the coordinate lines 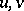 which form the principal base of the deformation. The spherical image of the principal base of the deformation coincides with the spherical image of the asymptotic lines of the Bianchi surface which is the rotation indicatrix (or the adjoined surface) of the infinitesimal deformation of
which form the principal base of the deformation. The spherical image of the principal base of the deformation coincides with the spherical image of the asymptotic lines of the Bianchi surface which is the rotation indicatrix (or the adjoined surface) of the infinitesimal deformation of 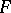 corresponding to the deformation over a principal base, as well as to the Clifford image of the asymptotic lines of a surface in an elliptic space (which is the rotations diagram of the deformation over a principal base of
corresponding to the deformation over a principal base, as well as to the Clifford image of the asymptotic lines of a surface in an elliptic space (which is the rotations diagram of the deformation over a principal base of  ).
).
Not all surfaces have a principal base; surfaces which allow of a deformation over a principal base form a special class of surfaces . A deformation over a kinematic base is a generalization of a deformation over a principal base; it is defined by the fact that the coefficients 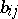 of the second fundamental form satisfy the equation
of the second fundamental form satisfy the equation 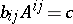 , where
, where 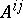 is a non-degenerate tensor and
is a non-degenerate tensor and  is a function depending on the metric
is a function depending on the metric 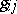 of the surface
of the surface 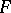 and on its derivatives.
and on its derivatives.
References
| [1] | K.M. Peterson, Mat. Sb. , 1 (1866) pp. 391–438 |
| [2] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 2 , Moscow-Leningrad (1948) (In Russian) |
| [3] | S.P. Finikov, "Deformation over a principal base and related problems in geometry" , Moscow-Leningrad (1937) (In Russian) |
| [4a] | N.N. Luzin, "Proof of a theorem in deformation theory" Izv. Akad. Nauk. SSSR Otd. Tekhn. Nauk , 2 (1939) pp. 81–105 (In Russian) |
| [4b] | N.N. Luzin, "Proof of a theorem in deformation theory" Izv. Akad. Nauk. SSSR Otd. Tekhn. Nauk , 7 (1939) pp. 115–132 (In Russian) |
| [4c] | N.N. Luzin, "Proof of a theorem in deformation theory" Izv. Akad. Nauk. SSSR Otd. Tekhn. Nauk , 10 (1939) pp. 65–84 (In Russian) |
Deformation over a principal base. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deformation_over_a_principal_base&oldid=15521