Etale cohomology
The cohomology of sheaves in the étale topology (cf. Etale topology). It is defined in the standard manner by means of derived functors. Let 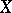 be a scheme and let
be a scheme and let 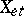 be the étale topology on
be the étale topology on 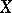 . Then the category of sheaves of Abelian groups on
. Then the category of sheaves of Abelian groups on  is an Abelian category with a sufficient collection of injective objects. The functor
is an Abelian category with a sufficient collection of injective objects. The functor 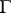 of global sections is left exact and its derived functors
of global sections is left exact and its derived functors 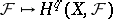 (where
(where 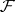 is a sheaf of Abelian groups on
is a sheaf of Abelian groups on 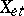 ) are called cohomology functors. Here
) are called cohomology functors. Here 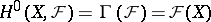 . Similarly, one defines the higher direct images
. Similarly, one defines the higher direct images 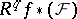 of
of 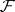 relative to a morphism
relative to a morphism 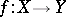 ; for them there is an analogue of the Leray spectral sequence. If
; for them there is an analogue of the Leray spectral sequence. If 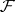 is a sheaf of non-Abelian groups, one can define the set
is a sheaf of non-Abelian groups, one can define the set 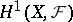 (see Non-Abelian cohomology).
(see Non-Abelian cohomology).
The most important results in the theory of étale cohomology are obtained for constructible étale sheaves of Abelian groups. Central among them is the finiteness theorem and the base-change theorem: Let 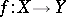 be a proper morphism and let
be a proper morphism and let  be a constructible sheaf on
be a constructible sheaf on 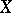 . Then the sheaves
. Then the sheaves 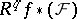 are constructible and the stalk of
are constructible and the stalk of 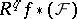 at a geometric point
at a geometric point 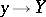 is isomorphic to the cohomology group
is isomorphic to the cohomology group 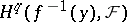 of the stalk
of the stalk 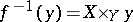 . Similar theorems are true for any morphism of finite type, provided that one uses cohomology with compact support.
. Similar theorems are true for any morphism of finite type, provided that one uses cohomology with compact support.
If 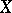 is an algebraic variety over an algebraically closed field, then for any constructible sheaf
is an algebraic variety over an algebraically closed field, then for any constructible sheaf 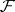 on
on 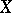 the cohomology groups with compact support
the cohomology groups with compact support 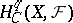 are finite and vanish for
are finite and vanish for 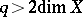 . If, in addition,
. If, in addition, 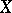 is an affine variety, then
is an affine variety, then 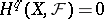 for
for 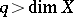 .
.
For varieties over the field of complex numbers the étale cohomology of constructible sheaves is the same as the classical cohomology with values in these sheaves. The specialization theorem for a smooth morphism holds: Suppose that 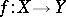 is a smooth proper morphism of schemes and that the integer
is a smooth proper morphism of schemes and that the integer  is invertible on
is invertible on 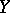 . Then the sheaves
. Then the sheaves 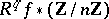 are locally constant on
are locally constant on 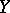 .
.
For étale cohomology there is an analogue of Poincaré duality (see Duality in algebraic geometry) and the Künneth formula. Every algebraic cycle of codimension  gives a cohomology class in dimension
gives a cohomology class in dimension 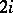 , which makes it possible to construct a theory of Chern classes (cf. Chern class).
, which makes it possible to construct a theory of Chern classes (cf. Chern class).
Etale cohomology of constructible sheaves is used to set up 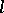 -adic cohomology and to prove the Weil conjecture on the zeta-function.
-adic cohomology and to prove the Weil conjecture on the zeta-function.
References
| [1] | A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , Proc. Internat. Math. Congress Edinburgh, 1958 , Cambridge Univ. Press (1960) pp. 103–118 |
| [2] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) |
| [3] | P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977) |
| [4] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie 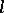 -adique et fonctions -adique et fonctions 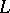 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) . SGA 5" , Lect. notes in math. , 589 , Springer (1977) |
| [5] | M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schémas (SGA 4) , Lect. notes in math. , 269; 270; 305 , Springer (1972–1973) |
Comments
References
| [a1] | P. Deligue, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–308 |
| [a2] | P. Deligue, "La conjecture de Weil II" Publ. Math. IHES , 52 (1980) pp. 137–252 |
Etale cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Etale_cohomology&oldid=15495