Chaplygin method
A method of approximately solving the initial value (Cauchy) problem for systems of ordinary differential equations of the first order, consisting in the simultaneous construction of two families of approximations to the solution. For example, in the case of the initial value (Cauchy) problem for a single equation of the first order
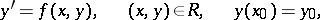 | (1) |
 |
one of these families approaches the solution from below, and the other from above.
At the basis of the method lies the Chaplygin theorem on differential inequalities. Let 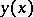 be a solution of (1) and suppose that the curves
be a solution of (1) and suppose that the curves 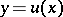 and
and 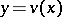 lie entirely inside the rectangle
lie entirely inside the rectangle 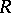 , pass through the point
, pass through the point 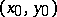 , and for
, and for 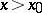 satisfy the inequalities
satisfy the inequalities
 |
Then for  the following inequalities hold:
the following inequalities hold:
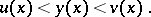 | (2) |
Functions 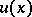 and
and 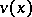 that satisfy the hypotheses of Chaplygin's theorem give upper and lower bounds for the solution to (1).
that satisfy the hypotheses of Chaplygin's theorem give upper and lower bounds for the solution to (1).
Given a pair of initial approximations 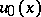 and
and 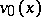 satisfying (2), Chaplygin's method enables one to construct a pair
satisfying (2), Chaplygin's method enables one to construct a pair 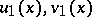 of closer approximations, satisfying
of closer approximations, satisfying
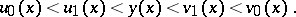 | (3) |
In the case where 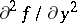 is of fixed sign throughout
is of fixed sign throughout  , the pair
, the pair 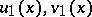 can be obtained as the solution of the pair of linear differential equations with initial condition
can be obtained as the solution of the pair of linear differential equations with initial condition 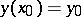 . If, for example,
. If, for example, 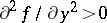 in
in 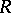 , then the curve of intersection of any plane
, then the curve of intersection of any plane 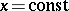 with the surface
with the surface 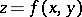 is convex from below, and any arc of that curve lies below the chord and above the tangent through any of its points. Suppose that for some
is convex from below, and any arc of that curve lies below the chord and above the tangent through any of its points. Suppose that for some 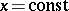 the equation of the tangent to the curve
the equation of the tangent to the curve  at the point
at the point 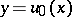 is
is
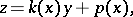 |
where
 |
and that the equation of the chord of the same curve joining the points 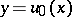 and
and  is
is
 |
where
 |
 |
Then for that value of  the inequalities
the inequalities
 | (4) |
hold. Condition (4) is satisfied uniformly for  in
in 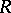 ; the solution
; the solution  to the initial value (Cauchy) problem
to the initial value (Cauchy) problem 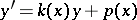 ,
, 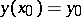 , and the solution
, and the solution  to the initial value (Cauchy) problem
to the initial value (Cauchy) problem 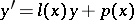 ,
, 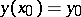 , satisfy condition (2). It can be shown that they also satisfy condition (3). Given the pair
, satisfy condition (2). It can be shown that they also satisfy condition (3). Given the pair 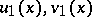 , one can construct in the same way a pair
, one can construct in the same way a pair  , etc. The process converges very quickly:
, etc. The process converges very quickly:
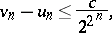 | (5) |
where the constant  depends neither on
depends neither on  nor on
nor on  .
.
A second way of constructing closer approximations 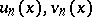 from given approximations
from given approximations 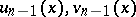 does not require the sign of
does not require the sign of 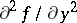 to be fixed in
to be fixed in 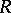 . In this method
. In this method
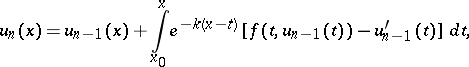 |
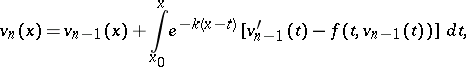 |
where 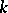 is the Lipschitz constant of
is the Lipschitz constant of 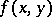 in
in 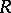 . In this case the pairs
. In this case the pairs 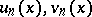 and
and 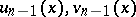 also satisfy condition (3) for all
also satisfy condition (3) for all  , but the rate of convergence is less than that given by (5).
, but the rate of convergence is less than that given by (5).
The main difficulty in the application of Chaplygin's method lies in the construction of initial approximations 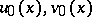 .
.
The method was proposed by S.A. Chaplygin in 1919.
References
| [1] | S.A. Chaplygin, "A new method of approximate integration of differential equations" , Moscow-Leningrad (1950) (In Russian) |
| [2] | N.N. Luzin, "On Academician S.A. Chaplygin's method of approximate integration" Trudy Ts.A.G.I. , 141 (1932) pp. 1–32 (In Russian) |
| [3] | S.G. Mikhlin, Kh.L. Smolitskii, "Approximate method for solution of differential and integral equations" , American Elsevier (1967) (Translated from Russian) |
Comments
References
| [a1] | L. Collatz, "The numerical treatment of differential equations" , Springer (1966) (Translated from German) |
Chaplygin method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chaplygin_method&oldid=15484