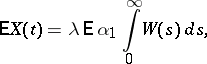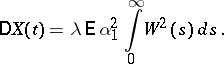A mathematical description of voltage fluctuations at the output of a linear system at the input of which there are random perturbations produced at random moments of time. If 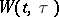 is the output of the system at time
is the output of the system at time 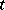 resulting from a single pulse applied at time
resulting from a single pulse applied at time 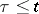 , the shot effect may be described by a stochastic process
, the shot effect may be described by a stochastic process
where 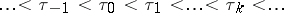 are the arrival moments of pulses, while
are the arrival moments of pulses, while 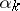 are random variables characterizing the magnitudes of the intensities of the pulses. In the particular case when
are random variables characterizing the magnitudes of the intensities of the pulses. In the particular case when  ,
, 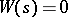 ,
, 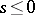 , the
, the 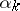 are independent, uniformly-distributed random variables with finite variance, while
are independent, uniformly-distributed random variables with finite variance, while 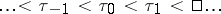 forms a Poisson flow of events with parameter
forms a Poisson flow of events with parameter 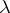 , the process
, the process 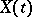 is a stationary stochastic process in the narrow sense, with
is a stationary stochastic process in the narrow sense, with
References
| [1] | J.H. Laning, R.G. Battin, "Random processes in automatic control" , McGraw-Hill (1956) |
References
| [a1a] | S.O. Rice, "Mathematical analysis of random noise" Bell Systems Techn. J. , 23 (1944) pp. 283–332 |
| [a1b] | S.O. Rice, "Mathematical analysis of random noise" Bell Systems Techn. J. , 24 (1945) pp. 46–156 |
| [a2] | N. Wax (ed.) , Selected papers on noise and stochastic processes , Dover, reprint (1953) |
| [a3] | E. Parzen, "Stochastic processes" , Holden-Day (1962) |
| [a4] | E. Wong, "Stochastic processes in information and dynamical systems" , McGraw-Hill (1971) |
How to Cite This Entry:
Shot effect. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shot_effect&oldid=15483
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article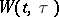 is the output of the system at time
is the output of the system at time 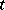 resulting from a single pulse applied at time
resulting from a single pulse applied at time 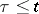 , the shot effect may be described by a stochastic process
, the shot effect may be described by a stochastic process
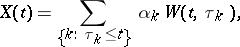
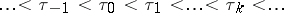 are the arrival moments of pulses, while
are the arrival moments of pulses, while 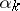 are random variables characterizing the magnitudes of the intensities of the pulses. In the particular case when
are random variables characterizing the magnitudes of the intensities of the pulses. In the particular case when  ,
, 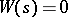 ,
, 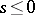 , the
, the 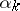 are independent, uniformly-distributed random variables with finite variance, while
are independent, uniformly-distributed random variables with finite variance, while 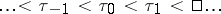 forms a Poisson flow of events with parameter
forms a Poisson flow of events with parameter 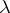 , the process
, the process 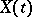 is a stationary stochastic process in the narrow sense, with
is a stationary stochastic process in the narrow sense, with