Dedekind-theorem(2)
From Encyclopedia of Mathematics
on linear independence of field homomorphisms, Dedekind lemma
Any set of field homomorphisms of a field 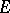 into another field
into another field 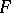 is linearly independent over
is linearly independent over 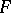 (see also Homomorphism; Linear independence). I.e., if
(see also Homomorphism; Linear independence). I.e., if  are distinct homomorphisms
are distinct homomorphisms 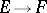 , then for all
, then for all  in
in 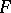 , not all zero, there is an
, not all zero, there is an 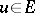 such that
such that
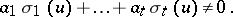 |
An immediate consequence is a basic estimate in Galois theory: If 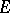 ,
, 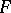 are field extensions of a field
are field extensions of a field 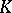 and the degree
and the degree 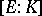 of
of 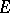 over
over 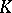 is
is  (cf. Extension of a field), than there are at most
(cf. Extension of a field), than there are at most 
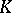 -homomorphisms of fields
-homomorphisms of fields 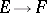 .
.
References
| [a1] | P.M. Cohn, "Algebra" , 2 , Wiley (1989) pp. 81 (Edition: Second) |
| [a2] | K.-H. Sprindler, "Abstract algebra with applications" , 2 , M. Dekker (1994) pp. 395 |
| [a3] | N. Jacobson, "Lectures in abstract algebra: Theory of fields and Galois theory" , 3 , v. Nostrand (1964) pp. Chap. I, §3 |
How to Cite This Entry:
Dedekind-theorem(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind-theorem(2)&oldid=15461
Dedekind-theorem(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dedekind-theorem(2)&oldid=15461
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article