Normal sheaf

An analogue to a normal bundle in sheaf theory. Let

be a morphism of ringed spaces such that the homomorphism 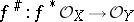is surjective, and let 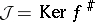. Then 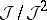is a sheaf of ideals in 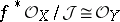and is, therefore, an 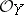-module. Here 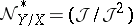is called the conormal sheaf of the morphism and the dual 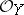-module 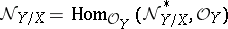is called the normal sheaf of the morphism . These sheaves are, as a rule, examined in the following special cases.

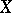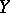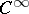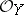1) and are differentiable manifolds (for example, of class ), and is an immersion. There is an exact sequence of -modules

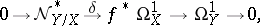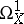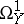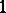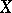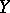where and are the sheaves of germs of smooth -forms on and , and 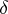is defined as differentiation of functions. The dual exact sequence

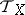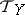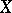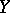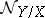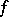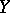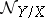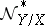where and are the tangent sheaves on and , shows that is isomorphic to the sheaf of germs of smooth sections of the normal bundle of the immersion . If is an immersed submanifold, then and are called the normal and conormal sheaves of the submanifold .

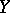2) 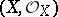is an irreducible separable scheme of finite type over an algebraically closed field 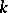, 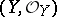is a closed subscheme of it and 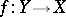is an imbedding. Then 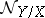and 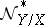are called the normal and conormal sheaves of the subscheme 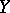. There is also an exact sequence of 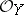-modules

(*)

where 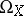and 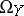are the sheaves of differentials on 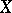and 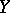. The sheaves 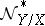and 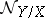are quasi-coherent, and if 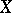is a Noetherian scheme, then they are coherent. If 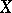is a non-singular variety over 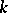and 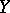is a non-singular variety, then 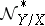is locally free and the homomorphism 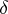in (*) is injective. In this case one obtains the dual exact sequence

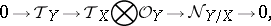so that the normal sheaf 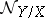is locally free of rank 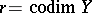corresponding to the normal bundle over 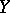. In particular, if 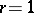, then 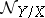is the invertible sheaf corresponding to the divisor .

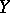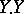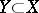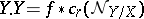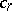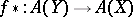In terms of normal sheaves one can express the self-intersection of a non-singular subvariety . Namely, , where is the -th Chern class and is the homomorphism of Chow rings (cf. Chow ring) corresponding to the imbedding .

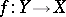3) 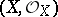is a complex space, 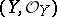is a closed analytic subspace of it and 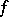is the imbedding. Then and 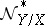are called the normal and conormal sheaves of the subspace 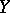; they are coherent. If 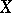is an analytic manifold and 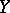an analytic submanifold of it, then 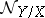is the sheaf of germs of holomorphic sections of the normal bundle over .

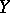References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[2]	R. Hartshorne, "Algebraic geometry" , Springer (1977)

Comments

If 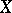is a non-singular variety over 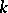and 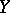is a subscheme of 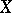that is locally a complete intersection, then 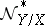is locally free.