Kronecker-Capelli theorem
From Encyclopedia of Mathematics
compatibility criterion for a system of linear equations
A system of equations
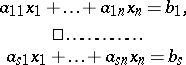 |
is compatible if and only if the rank of the coefficient matrix 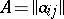 is equal to that of the augmented matrix
is equal to that of the augmented matrix 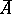 obtained from
obtained from 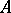 by adding the column of free terms
by adding the column of free terms 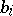 .
.
Kronecker's version of this theorem is contained in his lectures read at the University of Berlin in 1883–1891 (see [1]). A. Capelli was apparently the first to state the theorem in the above form, using the term "rank of a matrix" (see [2]).
References
| [1] | L. Kronecker, "Vorlesungen über die Theorie der Determinanten" , Leipzig (1903) |
| [2] | A. Capelli, "Sopra la compatibilitá o incompatibilitá di più equazioni di primo grado fra picì incognite" Revista di Matematica , 2 (1892) pp. 54–58 |
| [3] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
How to Cite This Entry:
Kronecker-Capelli theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker-Capelli_theorem&oldid=15427
Kronecker-Capelli theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker-Capelli_theorem&oldid=15427
This article was adapted from an original article by I.V. Proskuryakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article