Multiharmonic function
A harmonic function such that the Laplace operator acting on separate groups of independent variables vanishes. More precisely: A function  ,
,  , of class
, of class  in a domain
in a domain  of the Euclidean space
of the Euclidean space  is called a multiharmonic function in
is called a multiharmonic function in  if there exist natural numbers
if there exist natural numbers  ,
,  ,
,  , such that the following identities hold throughout
, such that the following identities hold throughout 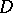 :
:
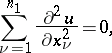 |
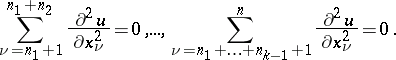 |
An important proper subclass of the class of multiharmonic functions consists of the pluriharmonic functions (cf. Pluriharmonic function), for which 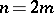 ,
,  ,
, 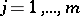 , i.e.
, i.e. 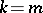 , and which also satisfy certain additional conditions.
, and which also satisfy certain additional conditions.
References
| [1] | E.M. Stein, G. Weiss, "Introduction to harmonic analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
Multiharmonic functions are also called multiply harmonic functions. It was shown by P. Lelong that if  is separately harmonic, that is,
is separately harmonic, that is,  is harmonic as a function of
is harmonic as a function of  (
( ;
; 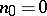 ) while the other variables remain fixed, then
) while the other variables remain fixed, then  is multiharmonic. A different proof is due to J. Siciak. See [a1].
is multiharmonic. A different proof is due to J. Siciak. See [a1].
References
| [a1] | M. Hervé, "Analytic and plurisubharmonic functions" , Lect. notes in math. , 198 , Springer (1971) |
Multiharmonic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiharmonic_function&oldid=15391