Inefficient statistic
inefficient estimator
A statistical estimator whose variance is greater than that of an efficient estimator. In other words, for an inefficient estimator equality in the Rao–Cramér inequality is not attained for at least one value of the parameter to be estimated. A quantitative measure of inefficiency of an inefficient estimator is the number  , the so-called efficiency, which is the ratio of the variance of an efficient estimator to that of the statistic in question. The efficiency
, the so-called efficiency, which is the ratio of the variance of an efficient estimator to that of the statistic in question. The efficiency  is non-negative and does not exceed 1. The quantity
is non-negative and does not exceed 1. The quantity 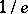 indicates by how much one has to increase the number of observations in using an inefficient estimator as compared with an efficient estimator so as to achieve equivalent results in the application of the two statistics. For example, the median
indicates by how much one has to increase the number of observations in using an inefficient estimator as compared with an efficient estimator so as to achieve equivalent results in the application of the two statistics. For example, the median  of an empirical distribution constructed from
of an empirical distribution constructed from  independent normally
independent normally 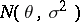 -distributed random variables
-distributed random variables 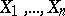 is asymptotically normally distributed with parameters
is asymptotically normally distributed with parameters 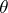 and
and 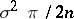 and is an inefficient order statistic estimating the expectation
and is an inefficient order statistic estimating the expectation 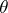 . In this case an efficient estimator is given by
. In this case an efficient estimator is given by 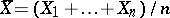 , which is distributed according to the normal law
, which is distributed according to the normal law 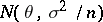 . The efficiency
. The efficiency  of the statistic
of the statistic 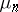 is
is
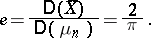 |
Consequently, in the use of the statistic 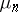 one has to make on the average
one has to make on the average 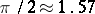 more observations as compared with
more observations as compared with 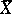 in order to obtain the same accuracy in the estimation of the unknown mathematical expectation
in order to obtain the same accuracy in the estimation of the unknown mathematical expectation  .
.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
There are also cases for which the minimal attainable variance of an estimator is larger than the Cramér–Rao bound, [a1].
References
| [a1] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) pp. 283 |
Inefficient statistic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inefficient_statistic&oldid=15359