Semi-group of operators
A family 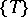 of operators on a Banach space or topological vector space with the property that the composite of any two operators in the family is again a member of the family. If the operators
of operators on a Banach space or topological vector space with the property that the composite of any two operators in the family is again a member of the family. If the operators 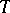 are "indexed" by elements of some abstract semi-group
are "indexed" by elements of some abstract semi-group 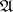 and the binary operation of the latter is compatible with the composition of operators,
and the binary operation of the latter is compatible with the composition of operators, 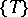 is known as a representation of the semi-group
is known as a representation of the semi-group 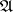 . The most detailed attention has been given to one-parameter semi-groups (cf. One-parameter semi-group) of bounded linear operators on a Banach space
. The most detailed attention has been given to one-parameter semi-groups (cf. One-parameter semi-group) of bounded linear operators on a Banach space 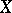 , which yield a representation of the additive semi-group of all positive real numbers, i.e. families
, which yield a representation of the additive semi-group of all positive real numbers, i.e. families 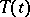 with the property
with the property
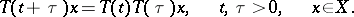 |
If 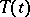 is strongly measurable,
is strongly measurable, 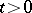 , then
, then 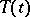 is a strongly-continuous semi-group; this will be assumed in the sequel.
is a strongly-continuous semi-group; this will be assumed in the sequel.
The limit
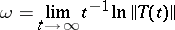 |
exists; it is known as the type of the semi-group. The functions 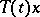 increase at most exponentially.
increase at most exponentially.
An important characteristic is the infinitesimal operator (infinitesimal generator) of the semi-group:
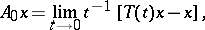 |
defined on the linear set 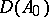 of all elements
of all elements  for which the limit exists; the closure,
for which the limit exists; the closure, 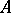 , of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let
, of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let 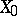 be the subspace defined as the closure of the union of all values
be the subspace defined as the closure of the union of all values 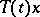 ; then
; then 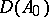 is dense in
is dense in 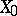 . If there are no non-zero elements in
. If there are no non-zero elements in 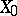 such that
such that 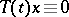 , then the generating operator
, then the generating operator 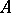 exists. In the sequel it will be assumed that
exists. In the sequel it will be assumed that  and that
and that 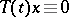 implies
implies  .
.
The simplest class of semi-groups, denoted by 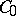 , is defined by the condition:
, is defined by the condition: 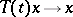 as
as 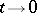 for any
for any 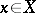 . This is equivalent to the condition: The function
. This is equivalent to the condition: The function 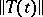 is bounded on any interval
is bounded on any interval 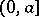 . In that case
. In that case 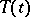 has a generating operator
has a generating operator 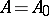 whose resolvent
whose resolvent 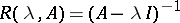 satisfies the inequalities
satisfies the inequalities
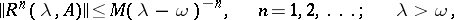 | (1) |
where 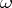 is the type of the semi-group. Conversely, if
is the type of the semi-group. Conversely, if 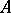 is a closed operator with domain of definition dense in
is a closed operator with domain of definition dense in 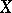 and with a resolvent satisfying (1), then it is the generating operator of some semi-group
and with a resolvent satisfying (1), then it is the generating operator of some semi-group 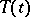 of class
of class 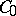 such that
such that 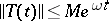 . Condition (1) is satisfied if
. Condition (1) is satisfied if
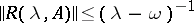 |
(the Hill–Yosida condition). If, moreover, 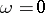 , then
, then  is a contraction semi-group:
is a contraction semi-group: 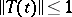 .
.
A summable semi-group is a semi-group for which the functions 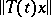 are summable on any finite interval for all
are summable on any finite interval for all 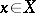 . A summable semi-group has a generating operator
. A summable semi-group has a generating operator 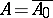 . The operator
. The operator 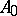 is closed if and only if, for every
is closed if and only if, for every 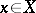 ,
,
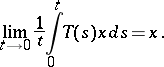 |
For 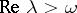 one can define the Laplace transform of a summable semi-group,
one can define the Laplace transform of a summable semi-group,
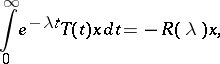 | (2) |
giving a bounded linear operator 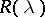 which has many properties of a resolvent operator.
which has many properties of a resolvent operator.
A closed operator 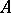 with domain of definition dense in
with domain of definition dense in 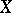 is the generating operator of a summable semi-group
is the generating operator of a summable semi-group 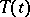 if and only if, for some
if and only if, for some 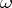 , the resolvent
, the resolvent 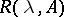 exists for
exists for 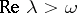 and the following conditions hold: a)
and the following conditions hold: a) 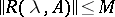 ,
, 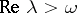 ; b) there exist a non-negative function
; b) there exist a non-negative function 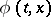 ,
, 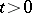 ,
,  , jointly continuous in all its variables, and a non-negative function
, jointly continuous in all its variables, and a non-negative function 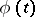 , bounded on any interval
, bounded on any interval 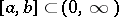 , such that, for
, such that, for 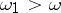 ,
,
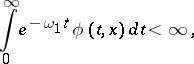 |
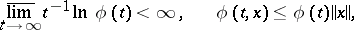 |
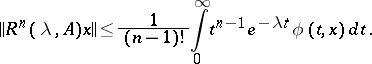 |
Under these conditions
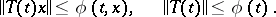 |
If one requires in addition that the function 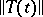 be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function
be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function 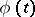 such that, for
such that, for 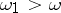 ,
,
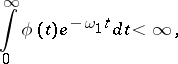 | (3) |
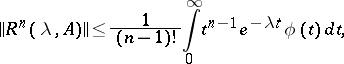 | (4) |
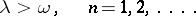 |
Under these conditions, 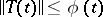 . By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If
. By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If 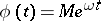 , the result is the class
, the result is the class 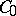 and (1) follows from (4). If
and (1) follows from (4). If 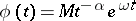 ,
, 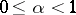 , condition (4) implies the condition
, condition (4) implies the condition
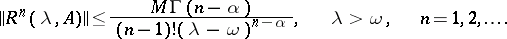 |
Semi-groups with power singularities.
If in the previous example 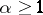 , then the integrals in (4) are divergent for
, then the integrals in (4) are divergent for 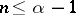 . Hence the generating operator for the corresponding semi-group may not have a resolvent for any
. Hence the generating operator for the corresponding semi-group may not have a resolvent for any 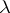 , i.e. it may have a spectrum equal to the entire complex plane. However, for
, i.e. it may have a spectrum equal to the entire complex plane. However, for  large enough one can define for such operators functions
large enough one can define for such operators functions 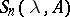 which coincide with the functions
which coincide with the functions 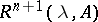 in the previous cases. The operator function
in the previous cases. The operator function 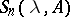 is called a resolvent of order
is called a resolvent of order  if it is analytic in some domain
if it is analytic in some domain 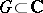 and if for
and if for 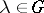 ,
,
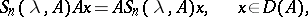 |
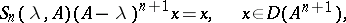 |
and if 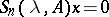 for all
for all 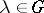 implies
implies 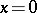 . If
. If 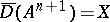 , the operator may have a unique resolvent of order
, the operator may have a unique resolvent of order  , for which there is a maximal domain of analyticity, known as the resolvent set of order
, for which there is a maximal domain of analyticity, known as the resolvent set of order  .
.
Let 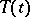 be a strongly-continuous semi-group such that the inequality
be a strongly-continuous semi-group such that the inequality
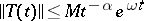 |
holds for 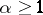 . Then its generating operator
. Then its generating operator 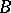 has a resolvent of order
has a resolvent of order  for
for 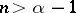 , and, moreover,
, and, moreover,
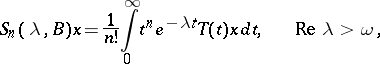 |
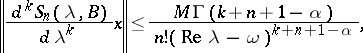 | (5) |
 |
Conversely, suppose that for 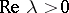 the operator
the operator 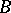 has a resolvent
has a resolvent 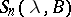 of order
of order  satisfying (5) with
satisfying (5) with 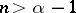 . Then there exists a unique semi-group
. Then there exists a unique semi-group 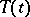 such that
such that
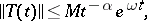 |
and the generating operator 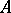 of this semi-group is such that
of this semi-group is such that 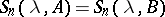 .
.
Smooth semi-groups.
If 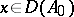 , the function
, the function  is continuously differentiable and
is continuously differentiable and
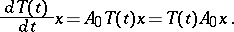 |
There exist semi-groups of class 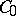 such that, if
such that, if 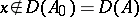 , the functions
, the functions 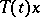 are non-differentiable for all
are non-differentiable for all 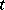 . However, there are important classes of semi-groups for which the degree of smoothness increases with increasing
. However, there are important classes of semi-groups for which the degree of smoothness increases with increasing 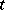 . If the functions
. If the functions 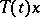 ,
, 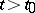 , are differentiable for any
, are differentiable for any 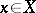 , then it follows from the semi-group property that the
, then it follows from the semi-group property that the 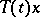 are twice differentiable if
are twice differentiable if 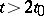 , three times differentiable if
, three times differentiable if 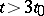 , etc. Therefore, if these functions are differentiable at any
, etc. Therefore, if these functions are differentiable at any 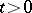 for
for 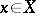 , then
, then 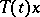 is infinitely differentiable.
is infinitely differentiable.
Given a semi-group of class 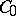 , a necessary and sufficient condition for the functions
, a necessary and sufficient condition for the functions 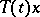 to be differentiable for all
to be differentiable for all 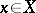 and
and 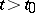 , where
, where 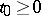 , is that there exist numbers
, is that there exist numbers 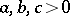 such that the resolvent
such that the resolvent 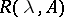 is defined in the domain
is defined in the domain
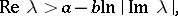 |
while in this domain
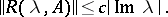 |
A necessary and sufficient condition for 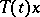 to be infinitely differentiable for all
to be infinitely differentiable for all 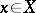 and
and 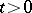 is that, for every
is that, for every 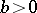 , there exist
, there exist 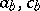 such that the resolvent
such that the resolvent 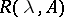 is defined in the domain
is defined in the domain
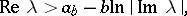 |
and such that
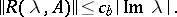 |
Sufficient conditions are: If there exists a 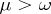 for which
for which
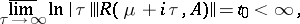 |
then the 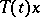 are differentiable for
are differentiable for 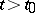 and
and 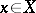 ; if
; if  , then the
, then the 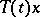 are infinitely differentiable for all
are infinitely differentiable for all 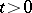 and
and 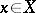 .
.
The degree of smoothness of a semi-group may sometimes be inferred from its behaviour at zero; for example, suppose that for every 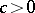 there exists a
there exists a 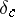 such that, for
such that, for 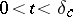 ,
,
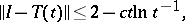 |
then the 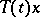 are infinitely differentiable for all
are infinitely differentiable for all 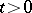 ,
, 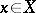 .
.
There are smoothness conditions for summable semi-groups and semi-groups of polynomial growth. If a semi-group has polynomial growth of degree 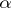 and is infinitely differentiable for
and is infinitely differentiable for 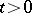 , then the function
, then the function
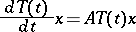 |
also has polynomial growth:
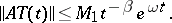 |
In the general case there is no rigorous relationship between the numbers 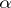 and
and 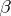 , and
, and 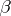 can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth.
can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth.
Analytic semi-groups.
An important class of semi-groups, related to partial differential equations of parabolic type, comprises those semi-groups 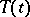 which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class
which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class 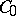 has this property if and only if its resolvent satisfies the following inequality in some right half-plane
has this property if and only if its resolvent satisfies the following inequality in some right half-plane 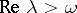 :
:
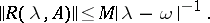 |
Another necessary and sufficient conditions is: The semi-group is strongly differentiable and its derivative satisfies the estimate
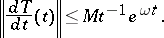 |
Finally, the inequality
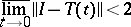 |
is also a sufficient condition for 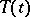 to be analytic.
to be analytic.
If a semi-group 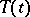 has an analytic continuation
has an analytic continuation 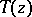 to a sector
to a sector 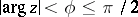 and has polynomial growth at zero,
and has polynomial growth at zero, 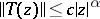 ,
, 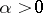 , then the resolvent
, then the resolvent 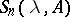 of order
of order 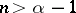 of its generating operator
of its generating operator 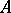 has an analytic continuation to the sector
has an analytic continuation to the sector 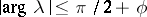 , and satisfies the following estimate in any sector
, and satisfies the following estimate in any sector 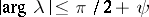 ,
, 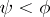 :
:
 |
Conversely, suppose that the resolvent 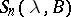 of an operator
of an operator 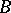 is defined in a sector
is defined in a sector 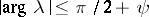 and that
and that
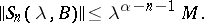 |
Then there exists a semi-group 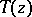 of growth
of growth 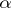 , analytic in the sector
, analytic in the sector 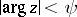 , whose generating operator
, whose generating operator 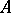 is such that
is such that 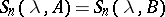 .
.
Distribution semi-groups.
In accordance with the general concept of the theory of distributions (cf. Generalized function), one can drop the requirement that the operator-valued function 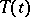 be defined for every
be defined for every 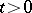 , demanding only that it be possible to evaluate the integrals
, demanding only that it be possible to evaluate the integrals 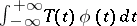 for all
for all 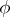 in the space
in the space 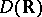 of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space
of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space 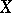 is a continuous linear mapping
is a continuous linear mapping  of
of 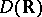 into the space
into the space  of all bounded linear operators on
of all bounded linear operators on 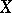 , with the following properties: a)
, with the following properties: a)  if
if  ; b) if
; b) if 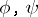 are functions in the subspace
are functions in the subspace 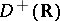 of all functions in
of all functions in 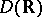 with support in
with support in 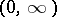 , then
, then 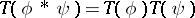 , where the star denotes convolution:
, where the star denotes convolution:
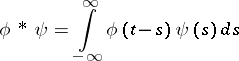 |
(the semi-group property); c) if 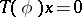 for all
for all 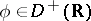 , then
, then 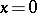 ; d) the linear hull of the set of all values of
; d) the linear hull of the set of all values of 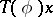 ,
, 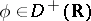 ,
, 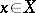 , is dense in
, is dense in 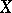 ; e) for any
; e) for any 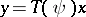 ,
, 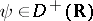 , there exists a continuous
, there exists a continuous 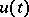 on
on 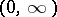 with values in
with values in 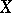 , so that
, so that 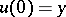 and
and
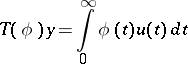 |
for all 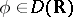 .
.
The infinitesimal operator 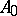 of a distribution semi-group is defined as follows. If there exists a delta-sequence
of a distribution semi-group is defined as follows. If there exists a delta-sequence 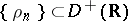 such that
such that 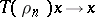 and
and 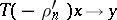 as
as  , then
, then 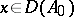 and
and 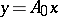 . The infinitesimal operator has a closure
. The infinitesimal operator has a closure 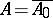 , known as the infinitesimal generator of the distribution semi-group. The set
, known as the infinitesimal generator of the distribution semi-group. The set 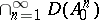 is dense in
is dense in 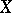 and contains
and contains  for any
for any 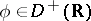 .
.
A closed linear operator 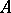 with a dense domain of definition in
with a dense domain of definition in 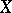 is the infinitesimal generator of a distribution semi-group if and only if there exist numbers
is the infinitesimal generator of a distribution semi-group if and only if there exist numbers 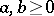 ,
, 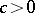 and a natural number
and a natural number  such that the resolvent
such that the resolvent 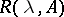 exists for
exists for 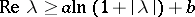 and satisfies the inequality
and satisfies the inequality
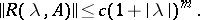 | (6) |
If 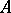 is a closed linear operator on
is a closed linear operator on 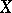 , then the set
, then the set 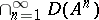 can be made into a Fréchet space
can be made into a Fréchet space 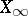 by introducing the system of norms
by introducing the system of norms
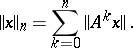 |
The restriction  of
of 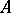 to
to 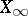 leaves
leaves 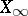 invariant. If
invariant. If 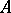 is the infinitesimal generator of a semi-group, then
is the infinitesimal generator of a semi-group, then  is the infinitesimal generator of a semi-group of class
is the infinitesimal generator of a semi-group of class 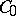 (continuous for
(continuous for 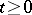 ,
, 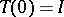 ) on
) on 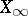 . Conversely, if
. Conversely, if 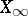 is dense in
is dense in  , the operator
, the operator 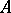 has a non-empty resolvent set and
has a non-empty resolvent set and 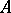 is the infinitesimal generator of a semi-group of class
is the infinitesimal generator of a semi-group of class 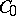 on
on 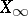 , then
, then 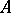 is the infinitesimal generator of a distribution semi-group on
is the infinitesimal generator of a distribution semi-group on 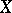 .
.
A distribution semi-group has exponential growth of order at most 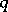 ,
,  , if there exists an
, if there exists an 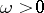 such that
such that 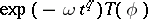 is a continuous mapping in the topology induced on
is a continuous mapping in the topology induced on  by the space
by the space 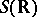 of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent
of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent 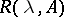 which satisfies (6) in the domain
which satisfies (6) in the domain
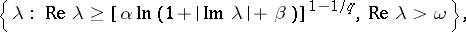 |
where 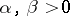 . In particular, if
. In particular, if 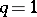 the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator
the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator 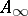 . Questions of smoothness and analyticity have also been investigated for distribution semi-groups.
. Questions of smoothness and analyticity have also been investigated for distribution semi-groups.
Semi-groups of operators in a (separable) locally convex space 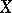 .
.
The definition of a strongly-continuous semi-group of operators 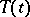 continuous on
continuous on 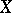 remains the same as for a Banach space. Similarly, the class
remains the same as for a Banach space. Similarly, the class 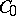 is defined by the property
is defined by the property 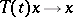 as
as 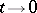 for any
for any 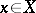 . A semi-group is said to be locally equicontinuous (of class
. A semi-group is said to be locally equicontinuous (of class 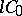 ) if the family of operators
) if the family of operators 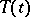 is equicontinuous when
is equicontinuous when 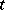 ranges over any finite interval in
ranges over any finite interval in 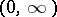 . In a barrelled space, a semi-group of class
. In a barrelled space, a semi-group of class 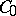 is always equicontinuous (cf. Equicontinuity).
is always equicontinuous (cf. Equicontinuity).
A semi-group is said to be equicontinuous (of class 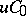 ) if the family
) if the family 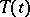 ,
, 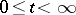 , is equicontinuous.
, is equicontinuous.
Infinitesimal operators and infinitesimal generators are defined as in the Banach space case.
Assume from now on that the space 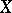 is sequentially complete. The infinitesimal generator
is sequentially complete. The infinitesimal generator 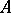 of a semi-group of class
of a semi-group of class 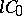 is identical to the infinitesimal operator; its domain of definition,
is identical to the infinitesimal operator; its domain of definition, 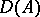 , is dense in
, is dense in 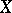 and, moreover, the set
and, moreover, the set 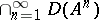 is dense in
is dense in 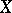 . The semi-group
. The semi-group 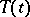 leaves
leaves 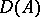 invariant and
invariant and
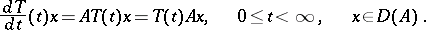 |
If 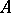 is the infinitesimal generator of a semi-group of class
is the infinitesimal generator of a semi-group of class 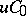 , the resolvent
, the resolvent 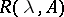 is defined for
is defined for 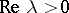 and is the Laplace transform of the semi-group.
and is the Laplace transform of the semi-group.
A linear operator 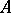 is the infinitesimal generator of a semi-group of class
is the infinitesimal generator of a semi-group of class  if and only if it is closed, has dense domain of definition in
if and only if it is closed, has dense domain of definition in 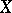 , and if there exists a sequence of positive numbers
, and if there exists a sequence of positive numbers 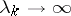 such that, for any
such that, for any 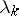 , the resolvent
, the resolvent 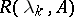 is defined and the family of operators
is defined and the family of operators 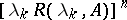 ,
, 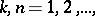 is equicontinuous. In this situation the semi-group can be constructed by the formula
is equicontinuous. In this situation the semi-group can be constructed by the formula
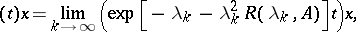 |
 |
In a non-normed locally convex space, the infinitesimal generator of a semi-group of class 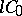 may have no resolvent at any point. An example is:
may have no resolvent at any point. An example is: 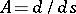 in the space
in the space 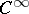 of infinitely-differentiable functions of
of infinitely-differentiable functions of  on
on 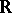 . As a substitute for the resolvent one can take a continuous operator whose product with
. As a substitute for the resolvent one can take a continuous operator whose product with 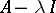 , from the right and the left, differs by a "small amount" from the identity operator.
, from the right and the left, differs by a "small amount" from the identity operator.
A continuous operator 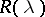 defined for
defined for 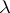 in a set
in a set 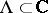 is called an asymptotic resolvent for a linear operator
is called an asymptotic resolvent for a linear operator 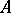 if
if 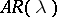 is continuous on
is continuous on 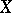 , the operator
, the operator 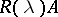 can be extended from
can be extended from 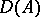 to a continuous operator
to a continuous operator 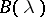 on
on 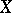 , and if there exists a limit point
, and if there exists a limit point 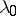 of the set
of the set 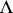 such that
such that 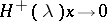 ,
, 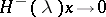 as
as 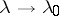 for any
for any 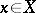 , where
, where
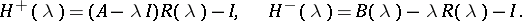 |
An asymptotic resolvent possesses various properties resembling those of the ordinary resolvent.
A closed linear operator 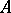 with a dense domain of definition in
with a dense domain of definition in 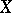 is the infinitesimal generator of a semi-group of class
is the infinitesimal generator of a semi-group of class 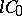 if and only if there exist numbers
if and only if there exist numbers 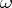 and
and 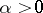 such that, for
such that, for 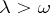 , there exists an asymptotic resolvent
, there exists an asymptotic resolvent 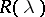 of
of 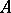 with the properties: the functions
with the properties: the functions 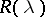 ,
, 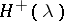 ,
, 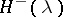 are strongly infinitely differentiable for
are strongly infinitely differentiable for 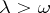 , and the families of operators
, and the families of operators
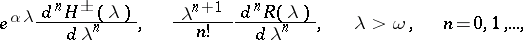 |
are equicontinuous.
Generation theorems have also been proved for other classes of semi-groups of operators on a locally convex space.
Adjoint semi-groups.
If 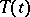 is a semi-group of class
is a semi-group of class 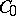 on a Banach space
on a Banach space 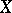 , then the adjoint operators form a semi-group of bounded operators on the adjoint space
, then the adjoint operators form a semi-group of bounded operators on the adjoint space  . However, the assertion that
. However, the assertion that 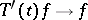 as
as 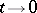 for any
for any 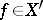 is valid only in the sense of the weak- topology
is valid only in the sense of the weak- topology  . If
. If  is the generating operator, its adjoint
is the generating operator, its adjoint 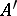 is a weak infinitesimal generator for
is a weak infinitesimal generator for 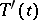 , in the sense that
, in the sense that 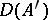 is the set of all
is the set of all 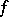 for which the limit of
for which the limit of 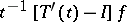 as
as 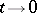 exists in the sense of weak- convergence and is equal to
exists in the sense of weak- convergence and is equal to  . The domain of definition
. The domain of definition 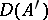 is dense in
is dense in 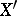 — again in the sense of the weak- topology — and the operator
— again in the sense of the weak- topology — and the operator 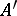 is closed in the weak- topology.
is closed in the weak- topology.
Let  be the set of all elements in
be the set of all elements in 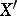 such that
such that 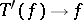 as
as 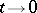 in the strong sense; then
in the strong sense; then 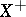 is a closed subspace of
is a closed subspace of 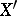 that is invariant under all
that is invariant under all 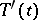 . On
. On 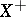 the operators
the operators  form a semi-group of class
form a semi-group of class 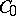 . The space
. The space 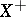 is also the strong closure of the set
is also the strong closure of the set 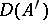 in
in 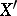 . If the original space is reflexive, then
. If the original space is reflexive, then 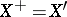 . Analogous propositions hold for semi-groups of class
. Analogous propositions hold for semi-groups of class 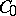 in locally convex spaces. Semi-groups of classes
in locally convex spaces. Semi-groups of classes 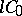 and
and 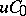 generate semi-groups of the same classes in
generate semi-groups of the same classes in 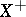 .
.
Distribution semi-groups in a (separable) locally convex space.
A distribution semi-group 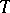 in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group
in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group  is said to be locally equicontinuous (of class
is said to be locally equicontinuous (of class 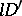 ) if, for any compact subset
) if, for any compact subset 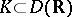 , the family of operators
, the family of operators 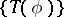 ,
, 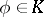 , is equicontinuous. In a barrelled space
, is equicontinuous. In a barrelled space 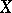 , any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class
, any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class 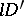 , the infinitesimal operator is closed
, the infinitesimal operator is closed 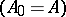 ,
, 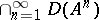 is dense in
is dense in 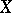 , and for any
, and for any 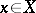 and
and 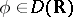 ,
,
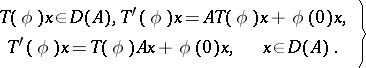 | (7) |
A generalized function 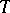 with support in
with support in 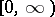 , possessing the properties (7), is naturally called the fundamental function of the operator
, possessing the properties (7), is naturally called the fundamental function of the operator 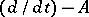 . Thus, if
. Thus, if 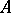 is the infinitesimal operator of a semi-group
is the infinitesimal operator of a semi-group 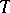 of class
of class 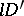 , then
, then 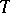 is the fundamental function of the operator
is the fundamental function of the operator 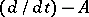 . The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function
. The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function 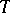 (or, more precisely, of the function
(or, more precisely, of the function 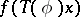 , where
, where 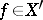 ).
).
A useful notion for the characterization of semi-groups in a locally convex space is that of the generalized resolvent. Let 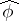 denote the Laplace transform of a function
denote the Laplace transform of a function 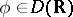 , and let
, and let 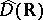 be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of
be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of 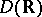 . The Laplace transform of an
. The Laplace transform of an 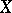 -valued generalized function
-valued generalized function 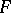 is defined by
is defined by 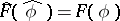 . Under these conditions,
. Under these conditions, 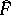 is a continuous mapping of
is a continuous mapping of 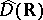 into the space
into the space 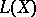 of continuous linear operators on
of continuous linear operators on 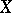 . Let
. Let 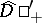 be the space of all
be the space of all 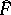 obtained from functions
obtained from functions 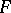 with support in
with support in 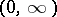 , with the natural topology. If
, with the natural topology. If 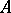 is a linear operator on
is a linear operator on 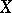 , it can be "lifted" to an operator
, it can be "lifted" to an operator 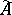 on
on 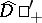 via the equality
via the equality
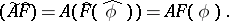 |
Thus, it is defined for all 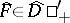 such that the right-hand side of the equality is defined for any
such that the right-hand side of the equality is defined for any 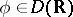 and it extends to a generalized function in
and it extends to a generalized function in 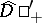 . The continuous operator
. The continuous operator 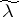 on
on  is defined by
is defined by
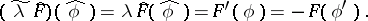 |
If the operator 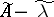 has a continuous inverse
has a continuous inverse 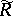 on
on 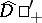 , then
, then 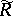 is called the generalized resolvent of
is called the generalized resolvent of 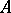 .
.
An operator 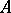 has a generalized resolvent if and only if the operator
has a generalized resolvent if and only if the operator 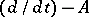 has a locally equicontinuous fundamental function
has a locally equicontinuous fundamental function 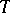 , constructed by the formula
, constructed by the formula
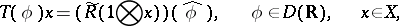 |
where
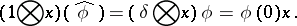 |
Subject to certain additional assumptions, 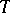 is a distribution semi-group. An extension theorem for semi-groups of class
is a distribution semi-group. An extension theorem for semi-groups of class 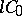 has also been proved in terms of generalized resolvents.
has also been proved in terms of generalized resolvents.
See also Semi-group of non-linear operators.
References
| [1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [2] | Yu.M. Vuvunikyan, "Evolutionary representations of algebras of generalized functions" , Theory of operators in function spaces , Novosibirsk (1977) pp. 99–120 (In Russian) |
| [3] | P.P. Zabreiko, A.V. Zafievskii, "On a certain class of semigroups" Soviet Math. Dokl. , 10 : 6 (1969) pp. 1523–1526 Dokl. Akad. Nauk SSSR , 189 : 5 (1969) pp. 934–937 |
| [4] | A.V. Zafievskii, Trudy Mat. Inst. Voronezh. Univ. , 1 (1970) pp. 206–210 |
| [5] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 |
| [6] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
| [7] | Yu.T. Sil'chenko, "An evolutionary equation with an operator generating a nonlinear semigroup" Differential Equations , 15 : 2 (1979) pp. 255–258 Differentsial'nye Uravneniya , 15 : 2 (1979) pp. 363–366 |
| [8] | J. Chazarain, "Problèmes de Cauchy abstracts et applications à quelques problèmes mixtes" J. Funct. Anal. , 7 : 3 (1971) pp. 386–446 |
| [9] | I. Ciorânescu, "La caracterisation spectrale d'opérateur, générateurs des semi-groupes distributions d'ordre fini de croissance" J. Math. Anal. Appl. , 34 (1971) pp. 34–41 |
| [10] | I. Ciorânescu, "A characterization of distribution semigroups of finite growth order" Rev. Roum. Math. Pures Appl. , 22 : 8 (1977) pp. 1053–1068 |
| [11] | T. Kato, "A characterization of holomorphic semigroups" Proc. Amer. Math. Soc. , 25 : 3 (1970) pp. 495–498 |
| [12] | J. Lions, "Les semigroupes distributions" Portugal. Math. , 19 (1960) pp. 141–164 |
| [13] | A. Pazy, "On the differentiability and compactness of semi-groups of linear operators" J. Math. Mech. , 17 : 12 (1968) pp. 1131–1141 |
| [14] | A. Pazy, "Approximations of the identity operator by semigroups of linear operators" Proc. Amer. Math. Soc. , 30 : 1 (1971) pp. 147–150 |
| [15] | T. Ushijima, "On the abstract Cauchy problems and semi-groups of linear operators in locally convex spaces" Sci. Papers College Gen. Educ. Univ. Tokyo , 21 (1971) pp. 93–122 |
| [16] | T. Ushijima, "On the generation and smoothness of semi-groups of linear operators" J. Fac. Sci. Univ. Tokyo, Sec. 1A , 19 : 1 (1972) pp. 65–127 |
| [17] | C. Wild, "Semi-groupes de croissance 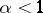 holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) |
| [18] | J.A. Gol'dstein, "Semigroups of linear operators and application" , Oxford Univ. Press (1985) (Translated from Russian) |
| [19] | A. Pazy, "Semigroups of linear operators and application to partial differential equations" , Springer (1983) |
| [20] | Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987) |
Comments
References
| [a1] | P. Butzer, H. Berens, "Semigroups of operators and approximation" , Springer (1967) |
| [a2] | H. Kellermann, M. Hieber, "Integrated semigroups" J. Funct. Anal. , 84 (1989) pp. 160–180 |
| [a3] | I. Miyadera, N. Tanaka, "Exponentially bounded  -semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 -semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 |
Semi-group of operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-group_of_operators&oldid=15341