Compact-open topology
One of the topologies on the set of mappings of one topological space into another. Let 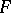 be some set of mappings of a topological space
be some set of mappings of a topological space 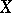 into a topological space
into a topological space 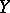 . Each finite collection of pairs
. Each finite collection of pairs 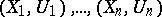 , where
, where 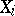 is a compact Hausdorff subset of
is a compact Hausdorff subset of 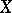 and
and 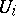 is an open subset of
is an open subset of 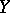 ,
, 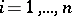 , determines the subset of mappings
, determines the subset of mappings 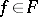 for which, for all
for which, for all  ,
, 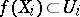 ; the family of all such sets is the base for the compact-open topology on
; the family of all such sets is the base for the compact-open topology on 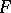 . The importance of compact-open topologies is due to the fact that they are essential elements in Pontryagin's theory of duality of locally compact commutative groups and participate in the construction of skew products. If
. The importance of compact-open topologies is due to the fact that they are essential elements in Pontryagin's theory of duality of locally compact commutative groups and participate in the construction of skew products. If 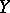 is a Hausdorff space, the compact-open topology also satisfies the Hausdorff separation axiom. If all mappings
is a Hausdorff space, the compact-open topology also satisfies the Hausdorff separation axiom. If all mappings 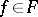 are continuous and if
are continuous and if 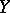 is a completely-regular space, then
is a completely-regular space, then 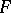 endowed with the compact-open topology is completely regular. On the assumption that all mappings
endowed with the compact-open topology is completely regular. On the assumption that all mappings 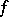 are continuous and that
are continuous and that 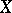 is a locally compact Hausdorff space, the compact-open topology on
is a locally compact Hausdorff space, the compact-open topology on 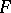 is admissible or compatible with continuity, i.e. the mapping
is admissible or compatible with continuity, i.e. the mapping 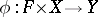 defined by the formula
defined by the formula 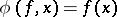 is continuous, and the compact-open topology is the smallest (weakest) of all topologies on
is continuous, and the compact-open topology is the smallest (weakest) of all topologies on  for which
for which 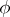 is continuous. In this respect the compact-open topology is preferable to the topology of pointwise convergence, since the latter is usually weaker than the former, and is not admissible in such a case. Moreover, the fact that the group of homeomorphisms of a Hausdorff compactum
is continuous. In this respect the compact-open topology is preferable to the topology of pointwise convergence, since the latter is usually weaker than the former, and is not admissible in such a case. Moreover, the fact that the group of homeomorphisms of a Hausdorff compactum 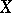 into itself, endowed with the compact-open topology, is a topological group which acts continuously (in the above sense) on
into itself, endowed with the compact-open topology, is a topological group which acts continuously (in the above sense) on 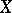 , is of fundamental importance. The group of homeomorphisms of an arbitrary locally compact Hausdorff space into itself need not be a topological group with respect to the compact-open topology (the transition to the inverse element may prove to be a discontinuous mapping with respect to this topology), but if a locally compact Hausdorff space
, is of fundamental importance. The group of homeomorphisms of an arbitrary locally compact Hausdorff space into itself need not be a topological group with respect to the compact-open topology (the transition to the inverse element may prove to be a discontinuous mapping with respect to this topology), but if a locally compact Hausdorff space 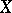 is locally connected, the compact-open topology again converts the group of all homeomorphisms of
is locally connected, the compact-open topology again converts the group of all homeomorphisms of 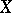 into itself into a topological group acting continuously on
into itself into a topological group acting continuously on  . This is an important result, since all manifolds are locally compact and locally connected.
. This is an important result, since all manifolds are locally compact and locally connected.
References
| [1] | J.L. Kelley, "General topology" , Springer (1975) |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [3] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [4] | R.F. Arens, "Topologies for homeomorphism groups" Amer. J. Math. , 68 : 4 (1946) pp. 593–610 |
Compact-open topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Compact-open_topology&oldid=15337