Linear complexity of a sequence
For a shift register sequence  , the linear complexity
, the linear complexity 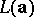 is just the degree of its minimal polynomial
is just the degree of its minimal polynomial 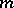 , i.e. the length of a shortest linear feedback shift register (LFSR; cf. Shift register sequence) capable of producing
, i.e. the length of a shortest linear feedback shift register (LFSR; cf. Shift register sequence) capable of producing  . The linear complexity also equals the maximum number of linearly independent vectors among the state vectors
. The linear complexity also equals the maximum number of linearly independent vectors among the state vectors
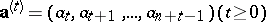 |
of an arbitrary LFSR of length  associated with
associated with  .
.
Now, let  denote either a finite sequence
denote either a finite sequence  of length
of length 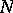 or an infinite sequence
or an infinite sequence 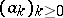 over a Galois field
over a Galois field 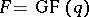 (in the latter case, put
(in the latter case, put 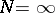 ). For every positive integer
). For every positive integer 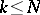 , denote by
, denote by 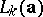 the length of an LFSR
the length of an LFSR 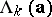 of least length over
of least length over 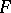 capable of producing a shift register sequence
capable of producing a shift register sequence  which agrees with
which agrees with  for the first
for the first 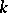 entries
entries 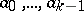 . In this way, one obtains a sequence
. In this way, one obtains a sequence 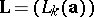 of the same length
of the same length 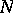 , which is called the linear complexity profile of
, which is called the linear complexity profile of  . Then one defines the linear complexity
. Then one defines the linear complexity 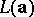 of
of  as the maximum value of all
as the maximum value of all 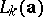 if these values are bounded, and as
if these values are bounded, and as 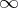 otherwise. Thus,
otherwise. Thus, 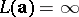 if and only if
if and only if  is an infinite sequence which is not ultimately periodic (cf. Ultimately periodic sequence), and
is an infinite sequence which is not ultimately periodic (cf. Ultimately periodic sequence), and 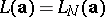 if
if  is a finite sequence of length
is a finite sequence of length 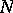 . Hence the linear complexity profile constitutes a refinement of the linear complexity of a sequence. The linear complexity profile of
. Hence the linear complexity profile constitutes a refinement of the linear complexity of a sequence. The linear complexity profile of  and the associated sequence of LFSRs
and the associated sequence of LFSRs 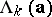 can be computed efficiently by the celebrated Berlekamp–Massey algorithm, see [a1] or [a2].
can be computed efficiently by the celebrated Berlekamp–Massey algorithm, see [a1] or [a2].
The linear complexity of a sequence is an important aspect in judging its suitability for use in cryptography. A high linear complexity by itself does not guarantee any randomness properties of the sequence considered. The linear complexity profiles of binary random sequences are analyzed in [a3], Chap. 4, where it is shown that a binary random sequence  of length
of length 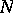 usually has linear complexity very close to
usually has linear complexity very close to 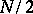 with the complexity profile growing in a roughly (but not exactly!) continuous manner (so that
with the complexity profile growing in a roughly (but not exactly!) continuous manner (so that 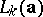 is close to
is close to  ). Moreover, using
). Moreover, using  to generate a periodic sequence
to generate a periodic sequence  with period
with period 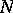 results in a linear complexity close to
results in a linear complexity close to 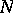 , provided that
, provided that 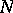 is a power of
is a power of  or a Mersenne prime number (cf. Mersenne number). Consequently, a periodic binary sequence with good randomness properties should have complexity close to the period length and a profile growing more or less smoothly.
or a Mersenne prime number (cf. Mersenne number). Consequently, a periodic binary sequence with good randomness properties should have complexity close to the period length and a profile growing more or less smoothly.
References
| [a1] | R.E. Blahut, "Theory and practice of error control codes" , Addison-Wesley (1983) |
| [a2] | D. Jungnickel, "Finite fields: Structure and arithmetics" , Bibliographisches Inst. Mannheim (1993) |
| [a3] | R. Rueppel, "Analysis and design of stream ciphers" , Springer (1986) |
Linear complexity of a sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_complexity_of_a_sequence&oldid=15334