Permutation group
A set of permutations (cf. Permutation of a set) of a set 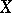 that form a group under the operation of multiplication (composition) of permutations. In other words, a permutation group is a pair
that form a group under the operation of multiplication (composition) of permutations. In other words, a permutation group is a pair 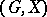 , where
, where 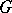 is a group and
is a group and 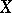 is a set, and each
is a set, and each 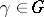 corresponds to a transformation
corresponds to a transformation  of
of  such that 1)
such that 1) 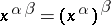 ,
, 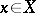 ,
, 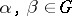 ; and 2)
; and 2) 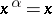 for all
for all 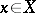 if and only if
if and only if  is the identity element of
is the identity element of 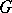 . If only condition 1) is fulfilled, one speaks of an action (or a representation) of
. If only condition 1) is fulfilled, one speaks of an action (or a representation) of 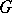 on
on 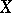 . In that case the subset
. In that case the subset 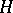 of elements of
of elements of  that leave invariant all
that leave invariant all 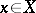 will be a normal subgroup of
will be a normal subgroup of 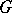 (called the kernel of the action), and the quotient group
(called the kernel of the action), and the quotient group 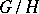 acts on
acts on 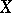 as a permutation group. If
as a permutation group. If 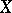 is a finite set, then a permutation group
is a finite set, then a permutation group  is called finite, otherwise infinite. The set of all permutations on
is called finite, otherwise infinite. The set of all permutations on 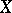 is called the symmetric group on
is called the symmetric group on 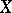 , and is denoted by
, and is denoted by 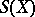 , or
, or 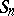 if
if  .
.
A similarity (or isomorphism) from a permutation group 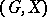 onto a permutation group
onto a permutation group 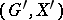 is a pair
is a pair  of mappings, where
of mappings, where 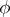 is an isomorphism from
is an isomorphism from 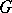 onto
onto 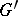 and
and 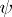 is a bijection from
is a bijection from 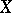 onto
onto 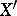 , where the two mappings fit in the sense that for all
, where the two mappings fit in the sense that for all 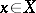 and
and 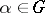 one has
one has 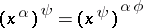 . Permutation groups between which there is a similarity are called similar. If
. Permutation groups between which there is a similarity are called similar. If 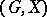 is a permutation group, there is a naturally defined equivalence on the set
is a permutation group, there is a naturally defined equivalence on the set 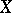 :
: 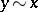 ,
, 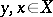 , if and only if
, if and only if 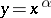 for some
for some 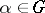 ; the equivalence classes of a permutation group are called orbits or sets of transitivity of the group
; the equivalence classes of a permutation group are called orbits or sets of transitivity of the group 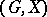 . A permutation group is transitive if it has only one orbit, while otherwise it is called intransitive. (See Transitive group.)
. A permutation group is transitive if it has only one orbit, while otherwise it is called intransitive. (See Transitive group.)
Any abstract group 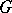 can be represented as a permutation group on a suitable set
can be represented as a permutation group on a suitable set 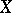 (Cayley's theorem). Here as
(Cayley's theorem). Here as 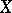 one may take the set of all elements of
one may take the set of all elements of 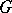 and put each
and put each 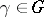 into correspondence with the mapping obtained by multiplication on the right by that element
into correspondence with the mapping obtained by multiplication on the right by that element 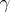 :
: 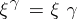 . The resulting regular representation of
. The resulting regular representation of 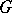 as a permutation group is not the only one possible. In research on permutation groups one is interested in properties different from those of interest in research on abstract groups. One is concerned not only with the group structure but primarily with how the group acts on the set
as a permutation group is not the only one possible. In research on permutation groups one is interested in properties different from those of interest in research on abstract groups. One is concerned not only with the group structure but primarily with how the group acts on the set 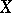 ; for example, the property of transitivity is a property of permutation groups, not of abstract groups.
; for example, the property of transitivity is a property of permutation groups, not of abstract groups.
Let 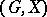 be a permutation group and
be a permutation group and 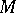 a subset of
a subset of 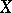 . The set of all permutations
. The set of all permutations 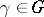 that map
that map  into itself (i.e.
into itself (i.e. 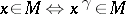 ) forms a subgroup
) forms a subgroup 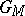 , called the stabilizer of the set
, called the stabilizer of the set 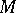 . The set of those permutations that leave invariant all individual
. The set of those permutations that leave invariant all individual 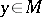 is called the pointwise stabilizer (or fixator) of the set
is called the pointwise stabilizer (or fixator) of the set 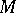 and is denoted by
and is denoted by 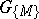 . The pointwise stabilizer is a normal subgroup of the stabilizer. If
. The pointwise stabilizer is a normal subgroup of the stabilizer. If 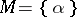 is a one-element set, the concepts of stabilizer and pointwise stabilizer coincide (the result is denoted by
is a one-element set, the concepts of stabilizer and pointwise stabilizer coincide (the result is denoted by 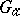 ). A permutation group is called semi-regular (or freely acting) if the stabilizer of each point is the identity group and regular (or simply transitive) if the group is also transitive. The centralizer
). A permutation group is called semi-regular (or freely acting) if the stabilizer of each point is the identity group and regular (or simply transitive) if the group is also transitive. The centralizer 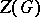 of a permutation group
of a permutation group  is defined as the centralizer of
is defined as the centralizer of 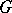 in the symmetric group
in the symmetric group 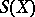 , i.e. the set of permutations on
, i.e. the set of permutations on 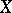 that commute with the elements of
that commute with the elements of 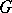 . The centralizer of a transitive group is semi-regular, and, conversely, the centralizer of a semi-regular group is transitive. A regular permutation group
. The centralizer of a transitive group is semi-regular, and, conversely, the centralizer of a semi-regular group is transitive. A regular permutation group 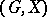 is similar to the above-described regular representation of the group
is similar to the above-described regular representation of the group 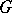 . The centralizer
. The centralizer 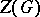 of the regular representation is the so-called left regular representation of
of the regular representation is the so-called left regular representation of 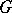 , which associates with the element
, which associates with the element 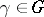 the permutation
the permutation 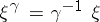 ,
, 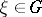 .
.
There are operations, [6], that enable one to construct new permutation groups from given ones.
a) The sum of permutation groups. Let 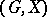 and
and 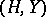 be two permutation groups with empty intersection
be two permutation groups with empty intersection 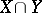 . The sum
. The sum 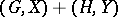 is defined as the permutation group consisting of the direct product
is defined as the permutation group consisting of the direct product 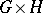 acting on the union
acting on the union  , where for
, where for 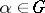 ,
, 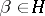 ,
, 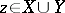 ,
,
 |
b) The product 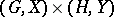 of two permutation groups
of two permutation groups 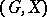 and
and 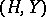 is the group
is the group 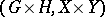 acting on
acting on 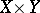 according to the formula
according to the formula 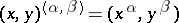 .
.
The two operations are associative and may be defined for any number of groups.
c) The wreath product. Let 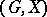 and
and 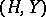 be two permutation groups and let
be two permutation groups and let 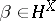 denote a mapping from
denote a mapping from  into
into 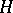 . On the set of pairs
. On the set of pairs 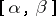 , which are called tables, a multiplication is defined by:
, which are called tables, a multiplication is defined by:
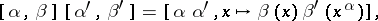 |
with respect to which they form a group 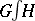 . The wreath product of the permutation groups
. The wreath product of the permutation groups 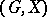 and
and 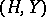 is the permutation group
is the permutation group 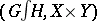 , where the action is defined by the formula
, where the action is defined by the formula
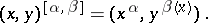 |
The wreath product is associative and may even be defined for any totally ordered family of permutation groups. The wreath product of non-identity permutation groups is an imprimitive group. If 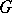 and
and 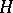 are taken in the guise of their regular representations, this concept coincides apart from the order of the factors with the usual group-theoretic wreath product.
are taken in the guise of their regular representations, this concept coincides apart from the order of the factors with the usual group-theoretic wreath product.
d) Exponentiation. The group of tables acting on the set 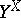 leads to the permutation groups
leads to the permutation groups
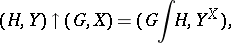 |
where the action is defined as follows:
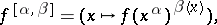 |
with 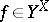 . Exponentiation is not associative and usually yields primitive groups, since
. Exponentiation is not associative and usually yields primitive groups, since 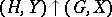 is primitive if
is primitive if 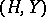 is a primitive non-cyclic group.
is a primitive non-cyclic group.
Permutation groups arise usually as groups of permutations preserving certain relations or operations on a set 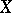 (see also Transformation group). For example, one source of the theory of permutation groups was the concept of the Galois group of a polynomial. If
(see also Transformation group). For example, one source of the theory of permutation groups was the concept of the Galois group of a polynomial. If
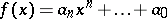 |
is a polynomial with coefficients 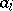 in some field
in some field 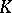 and
and 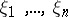 are the roots in some extension field, then the Galois group is the group of permutations of the set
are the roots in some extension field, then the Galois group is the group of permutations of the set 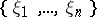 that preserve rational relations between the roots, i.e. equations of the form
that preserve rational relations between the roots, i.e. equations of the form
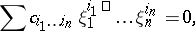 |
where 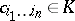 . E. Galois showed that the properties of this group govern the solvability of the equation
. E. Galois showed that the properties of this group govern the solvability of the equation 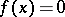 in radicals. This result led to developments in the theory of permutation groups by Galois, J. Serret, C. Jordan, and others. Further developments at the end of the nineteenth and the beginning of the 20th century were due to W. Burnside, W. Manning, G. Frobenius, O.Yu. Schmidt, and I. Schur. Permutation groups have many applications in discrete mathematics, for example in the classification of Boolean functions and finite automata, as well as in the theory of error-correcting codes and in counting the isomers of complicated organic compounds.
in radicals. This result led to developments in the theory of permutation groups by Galois, J. Serret, C. Jordan, and others. Further developments at the end of the nineteenth and the beginning of the 20th century were due to W. Burnside, W. Manning, G. Frobenius, O.Yu. Schmidt, and I. Schur. Permutation groups have many applications in discrete mathematics, for example in the classification of Boolean functions and finite automata, as well as in the theory of error-correcting codes and in counting the isomers of complicated organic compounds.
References
| [1] | D. Passman, "Permutation groups" , Benjamin (1968) |
| [2] | H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German) |
| [3] | W. Burnside, "Theory of groups of finite order" , Dover, reprint (1955) (Translated from German) |
| [4] | L.A. Kaluzhnin, V.I. Sushchanskii, "Transformations and permutations" , Moscow (1979) (In Ukrainian) |
| [5] | M. Hall, "Group theory" , Macmillan (1959) |
| [6] | L.A. Kaluzhnin, M.Kh. Klin, V.I. Sushchanskii, "Exponentiation of permutation groups I" Izv. Vyssch. Uchebn. Zaved. Mat. : 8 (1979) pp. 26–33 (In Russian) |
Permutation group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Permutation_group&oldid=15324