Homomorphism
A morphism in a category of algebraic systems (cf. Algebraic system). It is a mapping of an algebraic system  that preserves the basic operations and the basic relations. More exactly, let
that preserves the basic operations and the basic relations. More exactly, let  be an algebraic system with basic operations
be an algebraic system with basic operations  ,
,  , and with basic relations
, and with basic relations  ,
,  . A homomorphism from
. A homomorphism from  into a system
into a system  of the same type is a mapping
of the same type is a mapping  that satisfies the following two conditions:
that satisfies the following two conditions:
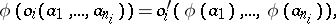 | (1) |
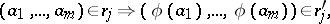 | (2) |
for all elements 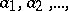 from
from 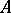 and all
and all 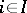 ,
,  .
.
E.g., if 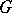 is a group and
is a group and 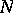 is a normal subgroup of it, then by assigning to each element
is a normal subgroup of it, then by assigning to each element 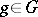 its coset
its coset  one obtains a homomorphism
one obtains a homomorphism 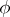 from
from 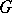 onto the quotient group
onto the quotient group 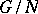 .
.
Suppose that each element 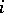 from
from  is brought into correspondence with some
is brought into correspondence with some 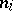 -ary function symbol
-ary function symbol 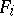 , while each element
, while each element 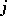 from
from 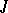 is brought into correspondence with an
is brought into correspondence with an 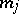 -place predicate symbol
-place predicate symbol 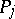 , and suppose that in each system
, and suppose that in each system  of the same type as
of the same type as  the result of the
the result of the 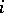 -th basic operation
-th basic operation  , applied to the elements
, applied to the elements  from
from 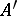 , is written as
, is written as 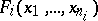 , while
, while  is denoted by
is denoted by  . Conditions (1), (2) are then simplified and take the form
. Conditions (1), (2) are then simplified and take the form
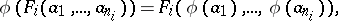 |
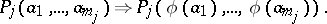 |
A homomorphism 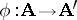 is called strong if for any elements
is called strong if for any elements 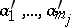 from
from  and for any predicate symbol
and for any predicate symbol  ,
, 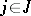 , the condition
, the condition  implies that there exist elements
implies that there exist elements 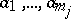 in
in  such that
such that  , and such that the relation
, and such that the relation 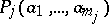 holds.
holds.
In the case of algebras the concepts of a homomorphism and a strong homomorphism coincide. For models there exist homomorphisms that are not strong, and one-to-one homomorphisms that are not isomorphisms (cf. Isomorphism).
If 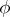 is a homomorphism of an algebraic system
is a homomorphism of an algebraic system 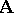 into an algebraic system
into an algebraic system 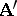 and
and  is the kernel congruence of
is the kernel congruence of 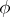 , then the mapping
, then the mapping 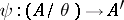 defined by the formula
defined by the formula 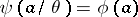 is a homomorphism of the quotient system
is a homomorphism of the quotient system 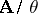 into
into 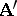 . If, in addition,
. If, in addition, 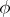 is a strong homomorphism, then
is a strong homomorphism, then 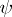 is an isomorphism. This is one of the most general formulations of the homomorphism theorem.
is an isomorphism. This is one of the most general formulations of the homomorphism theorem.
It should be noted that the name "homomorphism" is sometimes applied to morphisms in categories other than categories of algebraic systems (homomorphisms of graphs, sheaves, Lie groups).
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [2] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973) |
Comments
For example, a homomorphism  between two groups (cf. Group) is a mapping which commutes with the basic group-theoretic operations of multiplication, inversion and identity:
between two groups (cf. Group) is a mapping which commutes with the basic group-theoretic operations of multiplication, inversion and identity:
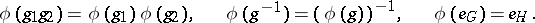 |
In this particular case it is well-known that the first of these conditions implies the other two, but in general the definition cannot be simplified in this way.
Homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homomorphism&oldid=15278