Natural equation

of a curve

A system of equations

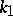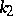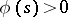defining the curvature and torsion of the curve as functions of the arc length parameter on the curve. For any regular functions and 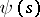there exists a curve, unique up to translation in space, with curvature 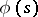and torsion 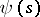. A necessary and sufficient condition for a curve to be in a plane is that its torsion vanishes identically. A necessary and sufficient condition for a curve to be a straight line (or a segment of a straight line) is that its curvature vanishes identically.

Comments

In the article above, 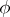must be positive in order to generate uniqueness of the curve; for existence 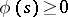suffices (cf. [a1], Sects. 8.5.8 and 8.6.15).

Instead of "natural equation" one also finds the phrase "intrinsic equation of a curveintrinsic equation of a curve" . The representation of (certain special) plane curves by means of a relation 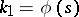goes back to L. Euler.

References

[a1]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a2]	M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976)
[a3]	B. O'Neill, "Elementary differential geometry" , Acad. Press (1966)
[a4]	M. Spivak, "A comprehensive introduction to differential geometry" , 2 , Publish or Perish pp. 1–5
[a5]	W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973)
[a6]	D.J. Struik, "Differential geometry" , Addison-Wesley (1950) pp. Sect. 1–8