Modulus of an automorphism
A positive real number associated to an automorphism of a locally compact group. Let  be such a group and let
be such a group and let  be an automorphism of
be an automorphism of  , regarded as a topological group. Then the modulus of
, regarded as a topological group. Then the modulus of  is defined by
is defined by
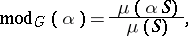 |
where  is left-invariant Haar measure on
is left-invariant Haar measure on  and
and  is any compact subset of
is any compact subset of  with positive measure (indeed,
with positive measure (indeed, 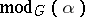 does not depend on
does not depend on 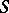 ). If
). If  is compact or discrete, then
is compact or discrete, then  , since for a compact group one can put
, since for a compact group one can put  , and for a discrete group one can take
, and for a discrete group one can take 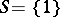 , where
, where 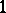 is the identity element of
is the identity element of 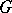 .
.
If 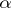 and
and 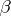 are two automorphism of
are two automorphism of 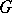 , then
, then
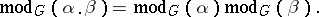 |
If 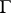 is a topological group which acts continuously on
is a topological group which acts continuously on  by automorphisms, then the associated homomorphism
by automorphisms, then the associated homomorphism 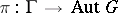 defines a continuous homomorphism
defines a continuous homomorphism 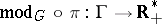 , where
, where  is the multiplicative group of positive real numbers. In particular, if
is the multiplicative group of positive real numbers. In particular, if  and
and 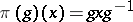 , then
, then 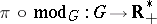 is a continuous homomorphism. This homomorphism is trivial if and only if the left-invariant Haar measure on
is a continuous homomorphism. This homomorphism is trivial if and only if the left-invariant Haar measure on 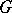 is simultaneously right invariant. Groups satisfying the latter condition are called unimodular.
is simultaneously right invariant. Groups satisfying the latter condition are called unimodular.
If  is a locally compact skew-field, then each non-zero element
is a locally compact skew-field, then each non-zero element  defines an automorphism
defines an automorphism  of the additive group of
of the additive group of  via multiplication by
via multiplication by  . The function
. The function 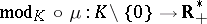 is used in the study of the structure of locally compact skew-fields.
is used in the study of the structure of locally compact skew-fields.
References
| [1] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [2] | A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940) |
| [3] | A. Weil, "Basic number theory" , Springer (1974) |
Modulus of an automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modulus_of_an_automorphism&oldid=15257