Normal extension

of a field

An algebraic field extension (cf. Extension of a field) of satisfying one of the following equivalent conditions:

1) any imbedding of in the algebraic closure of comes from an automorphism of ;

2) is the splitting field of some family of polynomials with coefficients in (cf. Splitting field of a polynomial);

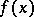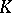3) any polynomial with coefficients in , irreducible over and having a root in 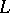, splits in 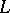into linear factors.

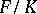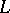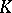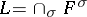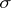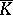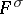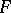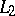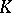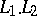For every algebraic extension there is a maximal intermediate subfield that is normal over ; this is the field , where ranges over all imbeddings of in . There is also a unique minimal normal extension of containing . This is the composite of all fields . It is called the normal closure of the field relative to . If and are normal extensions of , then so are the intersection and the composite . 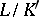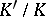However, when and are normal extensions, need not be normal.

For fields of characteristic zero every normal extension is a Galois extension. In general, a normal extension is a Galois extension if and only if it is separable (cf. Separable extension).

References

[1]	B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German)
[2]	S. Lang, "Algebra" , Addison-Wesley (1984)
[3]	M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian)