Butler group
A torsion-free Abelian group of finite rank (cf. Rank of a group) that is a pure subgroup of a completely decomposable group of finite rank. Equivalently, a Butler group is an epimorphic image of a completely decomposable group of finite rank [a5].
Clearly, all completely decomposable Abelian groups of finite rank are Butler groups, and so are their extensions by finite groups. There are lots of other examples of Butler groups. Let 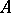 be a direct sum,
be a direct sum, 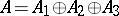 , where the
, where the 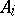 are rank-one torsion-free groups such that the elements
are rank-one torsion-free groups such that the elements 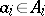 have characteristics
have characteristics 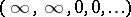 ,
, 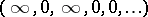 and
and 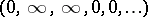 , respectively. The pure subgroup
, respectively. The pure subgroup 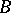 of
of 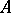 generated by the elements
generated by the elements 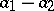 ,
, 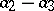 ,
, 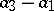 is a rank-two indecomposable Butler group. The class of Butler groups is closed under the formation of finite direct sums, pure subgroups and torsion-free epimorphic images. The type-set (i.e., the set of types of the non-zero elements) of a Butler group is always finite.
is a rank-two indecomposable Butler group. The class of Butler groups is closed under the formation of finite direct sums, pure subgroups and torsion-free epimorphic images. The type-set (i.e., the set of types of the non-zero elements) of a Butler group is always finite.
There are various other characterizations of Butler groups.
i) The following properties characterize Butler groups 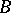 among the finite-rank torsion-free groups [a5]: a) the type-set of
among the finite-rank torsion-free groups [a5]: a) the type-set of 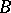 is finite; b) for each type
is finite; b) for each type 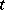 , the subgroup
, the subgroup 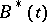 generated by the elements of type
generated by the elements of type 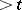 in
in 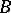 has finite index in its purification
has finite index in its purification 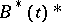 ; c) for each type
; c) for each type 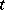 ,
, 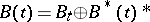 , where
, where 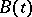 is the set of elements of type
is the set of elements of type 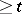 in
in 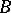 and
and 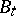 is a homogeneous completely decomposable group of type
is a homogeneous completely decomposable group of type 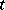 .
.
ii) A finite-rank torsion-free group 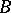 is a Butler group if and only if there is a partition
is a Butler group if and only if there is a partition 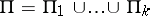 of the set
of the set 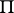 of prime numbers such that for each
of prime numbers such that for each 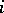 (
(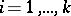 ), the tensor product
), the tensor product 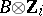 is a completely decomposable group with totally ordered type-set (here,
is a completely decomposable group with totally ordered type-set (here, 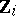 denotes the localization of
denotes the localization of 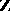 at the set
at the set 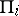 of primes) [a3].
of primes) [a3].
iii) A finite-rank torsion-free group 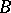 is Butler exactly if it satisfies
is Butler exactly if it satisfies 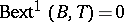 for all torsion Abelian groups
for all torsion Abelian groups 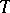 [a4]. Here,
[a4]. Here, 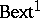 denotes the group of equivalence classes of extensions of
denotes the group of equivalence classes of extensions of 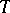 by
by 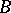 in which
in which 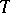 is a balanced subgroup.
is a balanced subgroup.
The classification of Butler groups has not gotten too far (1996). Two important classes have been characterized by invariants up to quasi-isomorphism. These are the Butler groups of Richman type [a13] and their duals. (A Butler group 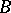 is of Richman type if it is a corank-one pure subgroup in a completely decomposable group of finite rank. See [a2], [a10], [a11].)
is of Richman type if it is a corank-one pure subgroup in a completely decomposable group of finite rank. See [a2], [a10], [a11].)
It is worthwhile mentioning that there is a close connection between Butler groups and representations of finite partially ordered sets.
Butler groups 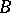 of countable rank were introduced in [a4]. Of the numerous equivalent characterizations, the following are noteworthy:
of countable rank were introduced in [a4]. Of the numerous equivalent characterizations, the following are noteworthy:
i) 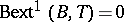 for all torsion Abelian groups
for all torsion Abelian groups 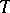 ;
;
ii) 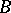 is the union of an ascending chain of (finite-rank) Butler subgroups which are pure in
is the union of an ascending chain of (finite-rank) Butler subgroups which are pure in 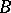 ;
;
iii) every finite-rank pure subgroup of 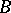 is a Butler group.
is a Butler group.
The study of Butler groups of large cardinalities often requires additional set-theoretical hypotheses beyond the axioms of ZFC (cf. Set theory). There are two kinds of Butler groups of arbitrary cardinality [a4]: 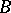 is a
is a 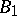 -group if
-group if 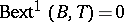 for all torsion Abelian groups
for all torsion Abelian groups  , and a
, and a 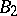 -group if it is the union of a continuous well-ordered ascending chain of pure subgroups
-group if it is the union of a continuous well-ordered ascending chain of pure subgroups 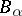 such that, for all
such that, for all 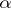 ,
, 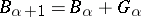 for some finite-rank Butler group
for some finite-rank Butler group  . All
. All 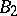 -groups are
-groups are 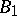 -groups, and the converse is one of the major open problems in Abelian group theory. It is known that the continuum hypothesis, CH, guarantees that all
-groups, and the converse is one of the major open problems in Abelian group theory. It is known that the continuum hypothesis, CH, guarantees that all 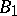 -groups of cardinality
-groups of cardinality  are
are 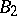 -groups [a6], while in Gödel's constructible universe
-groups [a6], while in Gödel's constructible universe 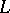 (cf. also Gödel constructive set), the same holds without cardinality restrictions [a9]. A useful criterion is: assuming CH, a
(cf. also Gödel constructive set), the same holds without cardinality restrictions [a9]. A useful criterion is: assuming CH, a 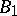 -group
-group 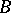 is a
is a 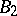 -group if and only if
-group if and only if 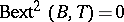 for all torsion groups
for all torsion groups 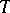 [a12].
[a12].
The other important problem is to find conditions under which a pure subgroup 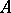 of a
of a 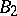 -group
-group 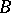 is likewise a
is likewise a 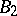 -group. A necessary and sufficient condition is the existence of a continuous well-ordered ascending chain of
-group. A necessary and sufficient condition is the existence of a continuous well-ordered ascending chain of 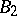 -subgroups from
-subgroups from 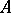 to
to 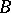 with rank-
with rank-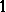 factors [a8]. A related problem is whether or not
factors [a8]. A related problem is whether or not 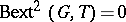 for all torsion-free groups
for all torsion-free groups  and all torsion groups
and all torsion groups  . In [a7] it is shown that CH is a necessary condition for the vanishing of
. In [a7] it is shown that CH is a necessary condition for the vanishing of 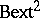 , while in [a9] it is proved that the hypothesis
, while in [a9] it is proved that the hypothesis 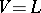 is a sufficient condition. It should be pointed out that
is a sufficient condition. It should be pointed out that 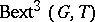 always vanishes, provided CH is assumed [a1]; more generally,
always vanishes, provided CH is assumed [a1]; more generally, 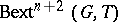 vanishes if
vanishes if 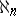 is the continuum for some integer
is the continuum for some integer 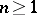 [a8]. Another useful result, valid in ZFC, states that in a balanced-projective resolution
[a8]. Another useful result, valid in ZFC, states that in a balanced-projective resolution 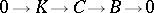 of a
of a 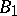 -group
-group 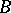 (i.e.,
(i.e., 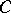 is completely decomposable and
is completely decomposable and  is balanced in
is balanced in 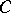 ), if one of
), if one of 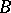 ,
, 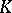 is a
is a 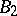 -group, then so is the other [a8].
-group, then so is the other [a8].
References
| [a1] | U. Albrecht, P. Hill, "Butler groups of infinite rank and Axiom 3" Czechosl. Math. J. , 37 (1987) pp. 293–309 |
| [a2] | D. Arnold, C. Vinsonhaler, "Invariants for a class of torsion-free abelian groups" Proc. Amer. Math. Soc. , 105 (1989) pp. 293–300 |
| [a3] | L. Bican, "Purely finitely generated abelian groups" Comment. Math. Univ. Carolin. , 21 (1980) pp. 209–218 |
| [a4] | L. Bican, L. Salce, "Butler groups of infinite rank" , Abelian Group Theory , Lecture Notes in Mathematics , 1006 , Springer (1983) pp. 171–189 |
| [a5] | M.C.R. Butler, "A class of torsion-free abelian groups of finite rank" Proc. London Math. Soc. , 15 (1965) pp. 680–698 |
| [a6] | M. Dugas, P. Hill, K.M Rangaswamy, "Infinite rank Butler groups II" Trans. Amer. Math. Soc. , 320 (1990) pp. 643–664 |
| [a7] | M. Dugas, B. Thomé, "The functor Bext and the negation of CH" Forum Math. , 3 (1991) pp. 23–33 |
| [a8] | L. Fuchs, "Butler groups of infinite rank" J. Pure Appl. Algebra , 98 (1995) pp. 25–44 |
| [a9] | L. Fuchs, M. Magidor, "Butler groups of arbitrary cardinality" Israel J. Math. , 84 (1993) pp. 239–263 |
| [a10] | L. Fuchs, C. Metelli, "On a class of Butler groups" Manuscr. Math. , 71 (1991) pp. 1–28 |
| [a11] | P. Hill, C. Megibben, "The classification of certain Butler groups" J. Algebra , 160 (1993) pp. 524–551 |
| [a12] | K.M. Rangaswamy, "A homological characterization of Butler groups" Proc. Amer. Math. Soc. , 121 (1994) pp. 409–415 |
| [a13] | F. Richman, "An extension of the theory of completely decomposable torsion-free abelian groups" Trans. Amer. Math. Soc. , 279 (1983) pp. 175–185 |
Butler group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Butler_group&oldid=15248