Special automorphism
constructed from an automorphism 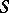 of a measure space
of a measure space 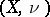 and a function
and a function 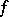 (defined on
(defined on 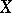 and taking positive integral values)
and taking positive integral values)
An automorphism 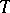 of a certain new measure space
of a certain new measure space  constructed in the following way. The points of
constructed in the following way. The points of 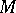 are the pairs
are the pairs  where
where  and
and  is an integer,
is an integer, 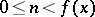 , and
, and 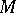 is equipped with the obvious measure
is equipped with the obvious measure 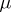 : if
: if 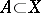 and
and 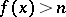 for all
for all  , then
, then 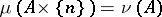 . If
. If 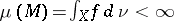 , then one usually normalizes this measure. Let
, then one usually normalizes this measure. Let 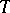 be the transformation that increases the second coordinate of the point
be the transformation that increases the second coordinate of the point 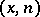 by one if
by one if 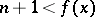 (i.e. if the transformed point remains within
(i.e. if the transformed point remains within 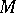 ), and otherwise put
), and otherwise put 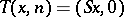 . The transformation
. The transformation 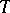 turns out to be an automorphism of the measure space
turns out to be an automorphism of the measure space 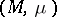 .
.
The above construction is often applied in ergodic theory when constructing various examples. On the other hand, the role of special automorphisms is clear from the following. By identifying each point 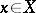 with
with 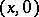 , one may assume that
, one may assume that 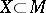 . Then
. Then 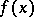 is the time spent by a point that starts in
is the time spent by a point that starts in 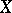 and moves under the action of the cascade
and moves under the action of the cascade 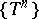 to return once again to
to return once again to 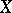 , and
, and 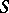 is the induced automorphism
is the induced automorphism 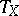 . Thus, special automorphisms can be used to recover the trajectories of a dynamical system in the whole phase space by observing only the passages of the moving point through the set
. Thus, special automorphisms can be used to recover the trajectories of a dynamical system in the whole phase space by observing only the passages of the moving point through the set 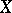 .
.
Comments
Instead of "special automorphism constructed from an automorphism S" one also speaks of a primitive of 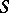 . (In that case what was called above the "induced automorphism" is called a derivative of
. (In that case what was called above the "induced automorphism" is called a derivative of 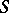 . See [a2].) The idea goes back to S. Kakutani; cf. [a1].
. See [a2].) The idea goes back to S. Kakutani; cf. [a1].
References
| [a1] | S. Kakutani, "Induced measure preserving transformations" Proc. Japan Acad. , 19 (1943) pp. 635–641 |
| [a2] | K. Petersen, "Ergodic theory" , Cambridge Univ. Press (1983) pp. 39 |
| [a3] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) pp. Chapt. 1, §5 (Translated from Russian) |
Special automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Special_automorphism&oldid=15242